Repère de Frenet 🔃

Introduction

Souvent on retrouve sur internet et dans certains ouvrages, la dérivation des formules des vitesses et accélérations dans le repère de Frenet utilisant un cercle (cas particulier) et des explications plus ou moins confuses. On se propose ici de démontrer proprement tout cela à l’aide de considération purement géométrique.

Présentation du repère

Le repère de Frenet, que l’on doit au mathématicien et astronome Jean Frédéric Frenet [1] [2] (1816 - 1900 à Périgueux) permet d’étudier les mouvements (en cinématique) des corps au voisinage local des courbes.

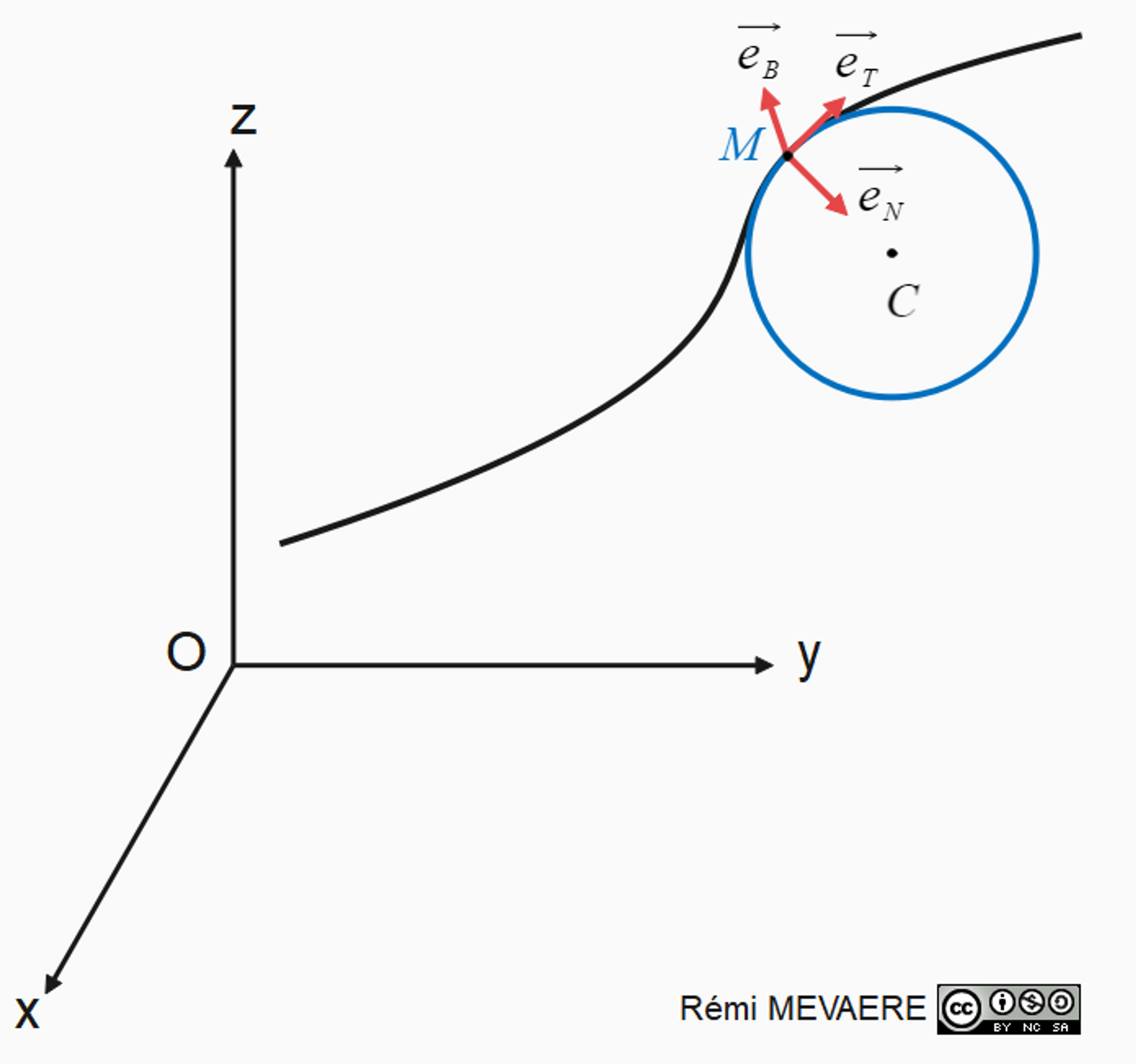
Le long d’une trajectoire quelconque, on peut définir localement en M un cercle osculateur (de centre C) qui vient épouser la courbure du mouvement. On défini alors une base locale pour décrire le mouvement en s’appuyant sur le trièdre de Frenet qui est défini par trois vecteurs \(\large (\vec{e_N},\vec{e_T},\vec{e_B})\).

• \(\large \vec{e_N}\) est un vecteur unitaire orienté de M vers C ;

• \(\large \vec{e_T}\) est un vecteur unitaire tangent à la trajectoire ;

• \(\large \vec{e_B}\) complète le trièdre direct.

Le référentiel d’étude est composé d’un repère d’espace \((O,x,y,z)\) et d’une horloge.

Dérivation de la formule de la vitesse

La vitesse est par définition relative à un référentiel, ici \(\mathcal{R}\) :

\[ \large \overrightarrow{V_{A/\mathcal{R}}}=\left(\frac{d\overrightarrow{OA}}{dt} \right)_\mathcal{R}=\left(\frac{d\overrightarrow{OA}}{ds} \right)_\mathcal{R}\left(\frac{ds}{dt}\right)_\mathcal{R} \]

Pour dériver convenablement la formule donnant la vitesse, il faut décrire convenablement la géométrie du problème, sans en restreindre trop la généralité. Ce que je présente ci-dessous en effectuant un agrandissement.

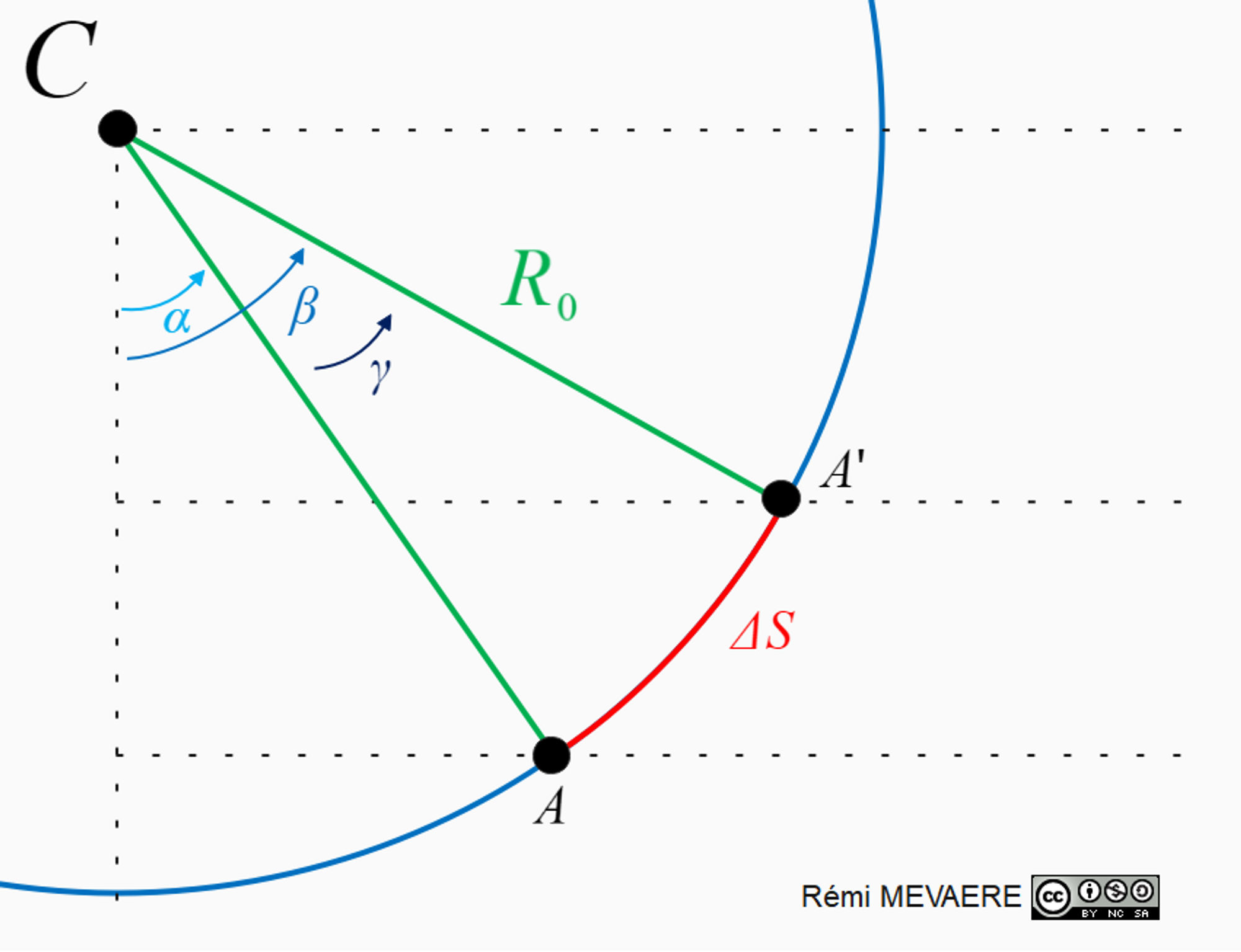
Pour notre démonstration on passe d’un élément différentiel, infiniment petit \(d\overrightarrow{OA}\) à un élément plus grand et plus accessible pédagogiquement \(\Delta \overrightarrow{OA}\) qui est la variation du vecteur \(\overrightarrow{OA}\) entre \(t\) et \(t+ dt\).

\[ \large \Delta \overrightarrow{OA} \approx \overrightarrow{OA}(t+dt) - \overrightarrow{OA}(t) \]

\[ \large \Delta \overrightarrow{OA} \approx \overrightarrow{OA'} - \overrightarrow{OA} = \overrightarrow{AA'} \]

Pour une petite variation, on peut approximer au premier ordre que :

\[ \large \Delta S \approx ||\overrightarrow{AA'}|| = AA' \]

\[ \large \overrightarrow{V_{A/\mathcal{R}}}=\left(\frac{d\overrightarrow{OA}}{ds} \right)_\mathcal{R}\left(\frac{ds}{dt}\right)_\mathcal{R}\approx \left(\frac{ds}{dt}\right)_\mathcal{R}\left( \frac{\Delta \overrightarrow{OA}}{\Delta S} \right)_\mathcal{R} \approx \left(\frac{ds}{dt}\right)_\mathcal{R}\left( \frac{ \overrightarrow{AA'}}{AA'} \right)_\mathcal{R} =\mathcal{v} \cdot \vec{e_T} \]

On obtient alors la vitesse de l’objet A dans le référentiel \(\mathcal{R}\), cette vitesse est tangente à la trajectoire.

\[ \Large \overrightarrow{V_{A/\mathcal{R}}}=\mathcal{v} \cdot \overrightarrow{e_T} \]

Dérivation de la formule de l’accélération

\[ \large \overrightarrow{V_{A/\mathcal{R}}}=\mathcal{v} \cdot \overrightarrow{e_T} \]

Pour obtenir l’accélération, en cinématique on dérive par rapport au temps :

\[ \large \overrightarrow{a_{A/\mathcal{R}}}=\left(\frac{d\mathcal{v}}{dt} \right)_\mathcal{R}\vec{e_T} + \mathcal{v} \left(\frac{d\mathcal{\vec{e_T}}}{dt} \right)_\mathcal{R} \]

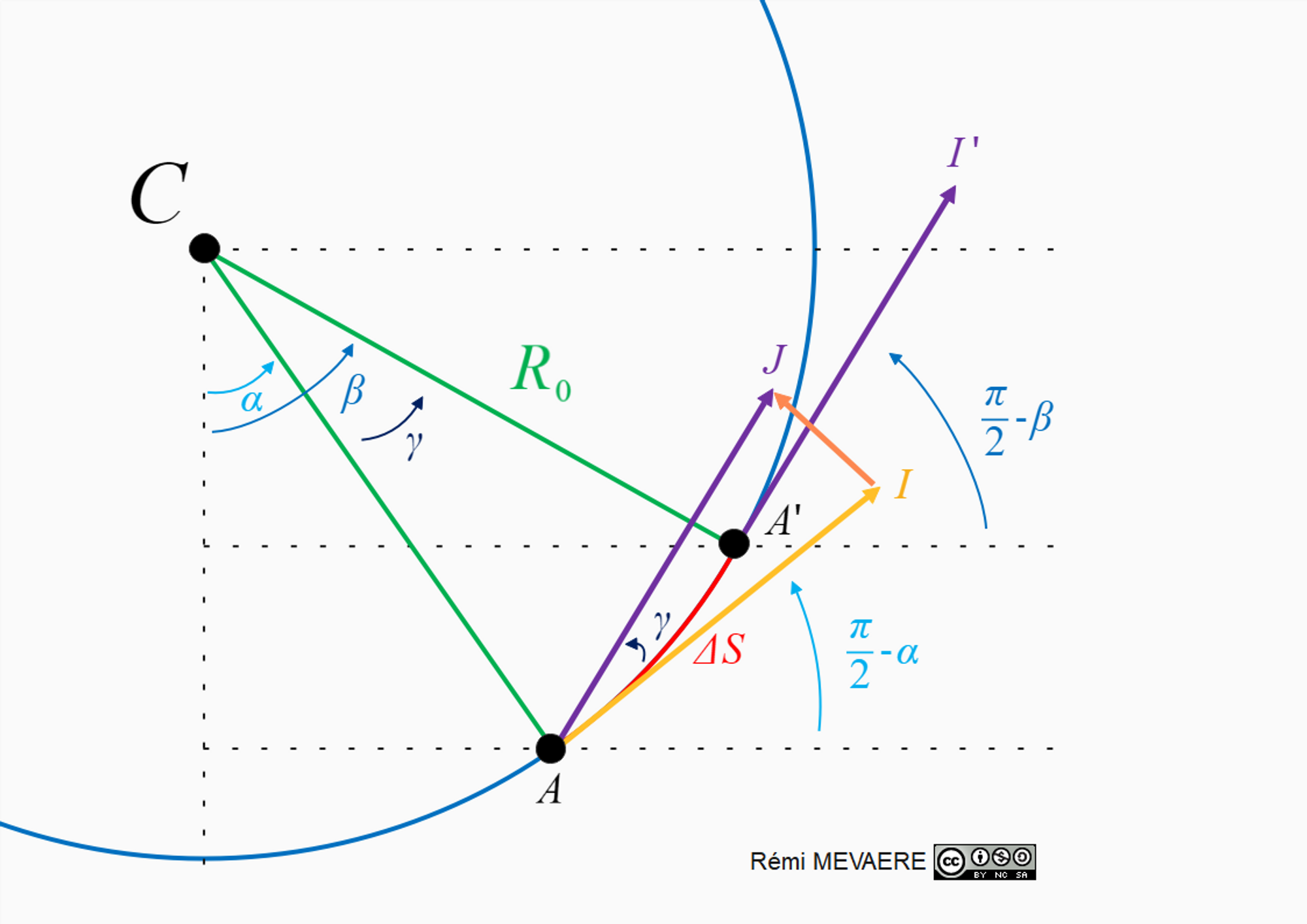
Il faut prendre son temps ici pour bien saisir, on exagère vraiment la taille des angles \(\alpha\) et \(\beta\). On pose le point \(\large J\) depuis \(\large \overrightarrow{A’I’} = \overrightarrow{A’J}\). L’angle \(\large \gamma = \beta - \alpha = \widehat{IAJ}\). Comme précédemment et pour le deuxième membre on cherche la variation du vecteur \(\large \Delta \vec{e_T}\) :

\[ \large \Delta \overrightarrow{e_T} = \overrightarrow{A'I'} - \overrightarrow{AI} =\overrightarrow{AJ} -\overrightarrow{AI} \]

\[ \large \Delta \overrightarrow{e_T} = \overrightarrow{IJ}=IJ \cdot \vec{e_N} \]

Or géométriquement :

\[ \large IJ = 2 \cdot sin\left( \frac{\gamma}{2} \right) \approx 2 \times \frac{\gamma}{2} = \gamma = \frac{\Delta S}{R_0} \]

\[ \large \Delta \overrightarrow{e_T} = \frac{\Delta S}{R_0} \cdot \overrightarrow{e_N} \implies \frac{\Delta \overrightarrow{e_T}}{\Delta S} = \frac{\overrightarrow{e_N}}{R_0} \implies \frac{d \overrightarrow{e_T}}{d s} = \frac{d \overrightarrow{e_N}}{R_0} \]

\[ \large \overrightarrow{a}_{A/\mathcal{R}}=\left(\frac{d\mathcal{v}}{dt} \right)_\mathcal{R}\overrightarrow{e_T} + \mathcal{v} \left(\frac{d\mathcal{\overrightarrow{e_T}}}{dt} \right)_\mathcal{R} \]

\[ \large \overrightarrow{a}_{A/\mathcal{R}}= a_T\cdot \overrightarrow{e_T} + \mathcal{v} \left(\frac{d\mathcal{\overrightarrow{e_T}}}{ds} \right)_\mathcal{R}\left(\frac{ds}{dt}\right)_\mathcal{R} = a_T\cdot \overrightarrow{e_T} + \mathcal{v} \cdot v \cdot \left(\frac{d\mathcal{\overrightarrow{e_T}}}{ds} \right)_\mathcal{R} \]

\[ \large \overrightarrow{a}_{A/\mathcal{R}}= a_T\cdot \overrightarrow{e_T} + \mathcal{v}^2 \left(\frac{\mathcal{\overrightarrow{e_N}}}{R_0} \right)_\mathcal{R} \]

Le tout permet d’obtenir la formule des accélérations dans la base de Frenet. Le premier membre correspond à ==l’accélération tangentielle== et le deuxième à ==l’accélération centripète== ressentie comme une force centrifuge pour la personne présente dans le référentiel \(\mathcal{R}\).

\[ \Large \overrightarrow{a_{A/\mathcal{R}}}= \frac{d\mathcal{v}}{dt}\cdot \overrightarrow{e_T} + \frac{\mathcal{v}^2}{R_0}\cdot \overrightarrow{e_N} \]

Sources et autres liens

---

[1]

Wikipédia, Jean Frédéric Frenet

[2]

Wikipédia, Repère de Frenet

[3]

Mécanique - J.-Ph Pérez - 7ed