For Science 🔭

Why I Choose to Use Python 🐍 for Science 🔭

Story

From Childhood to Code

As a child, I began my journey into programming by developing software in VB6 and Delphi 7-Xe2. It was a thrilling hobby, allowing me to create GUI applications with ease and develop great softwares using these tools. However, these environments had their downsides. They often masked underlying complexities, and I didn’t learn much about algorithms or data structures. I was simply translating my ideas into code without truly understanding the mechanics. This approach wasn’t conducive to performance or a deep understanding of how things work. Learning C/C++ felt like a chore because it wasn’t as gratifying; development was slow, and the programs often looked ugly (console).

From Hobbies to Studies

My academic journey led me to study Physics and Chemistry. Here, I delved into understanding how things work, from the basics of transistors to the principles of physics—what our ancient ancestors called « nature. » As I gained more confidence in my knowledge, I dabbled in Assembly 86x64 with AVX2, C, and C++. Despite my efforts to find the perfect programming language, success eluded me. Becoming a first-class developer requires an intimate understanding of architecture and more. Creating a Software as a Service (SaaS) with a Python backend and a JavaScript frontend doesn’t demand top-tier performance, but that isn’t my goal.

The Quest for Practicality

My goal is to use my computer to solve physics problems and create small simulations and tools for my students. Python emerged as the ideal choice for this purpose. It’s versatile, easy to learn, and supported by a vast ecosystem of libraries suited for scientific computing. Python allows me to efficiently translate complex scientific concepts into code, providing a balance between ease of use and powerful capabilities.

Another small benchmark

In this brief article, I want to illustrate the ease or difficulty of using common libraries and explain why I have decided to abandon C++ for my teaching activities as a physics teacher.

The bench

For instance, consider the task of multiplying two 3000x3000 matrices, a common problem in scientific computing. In Python, using libraries like NumPy, this task becomes straightforward and efficient. See how this task is done in C++.

Beginner approach

Python with Numpy

import numpy as np
import time

# Create large matrices
a = np.random.rand(3000, 3000)
b = np.random.rand(3000, 3000)

# Time the matrix multiplication
start = time.time()
c = np.dot(a, b)
end = time.time()

print(f"Time taken by NumPy: {end - start} seconds")

Astuce

Results for Python / Numpy : 0.1469 seconds

C++ - Naïve - MSVC

cmake_minimum_required(VERSION 3.28)  
project(Simple)  

set(CMAKE_CXX_STANDARD 17)  

# Add optimization flags for Release build type  
set(CMAKE_CXX_FLAGS_RELEASE "${CMAKE_CXX_FLAGS_RELEASE} /O2 /Ox")
add_executable(Simple main.cpp)  

#include <iostream>
#include <vector>
#include <chrono>

void matmul(const std::vector<std::vector<double>>& A,
            const std::vector<std::vector<double>>& B,
            std::vector<std::vector<double>>& C) {
    int n = A.size();
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            C[i][j] = 0;
            for (int k = 0; k < n; ++k) {
                C[i][j] += A[i][k] * B[k][j];
            }
        }
    }
}

int main() {
    int n = 3000;
    std::vector<std::vector<double>> A(n, std::vector<double>(n));
    std::vector<std::vector<double>> B(n, std::vector<double>(n));
    std::vector<std::vector<double>> C(n, std::vector<double>(n));

    // Initialize matrices
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            A[i][j] = rand() / double(RAND_MAX);
            B[i][j] = rand() / double(RAND_MAX);
        }
    }

    auto start = std::chrono::high_resolution_clock::now();
    matmul(A, B, C);
    auto end = std::chrono::high_resolution_clock::now();

    std::chrono::duration<double> duration = end - start;
    std::cout << "Time taken by C++: " << duration.count() << " seconds" << std::endl;

    return 0;
}

Astuce

Results for C++ / Naïve : 55.9159 seconds

How to explain the differences between the two ?

To inspect and study this, we will use Intel VTune profiler

Numpy

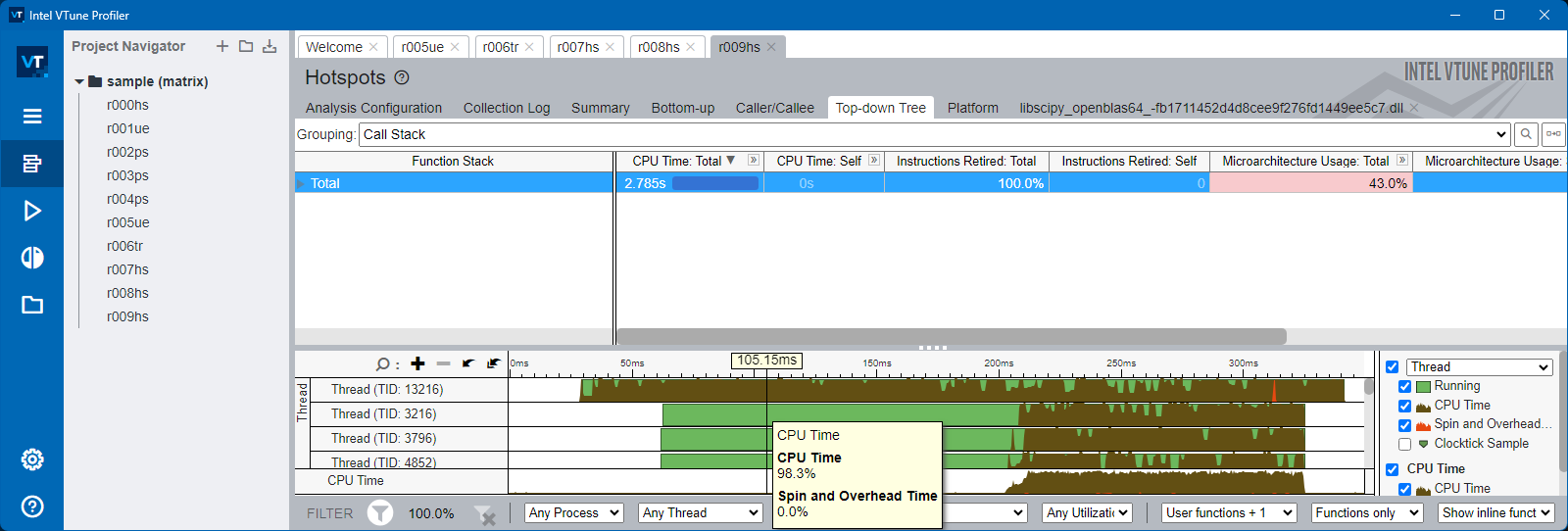
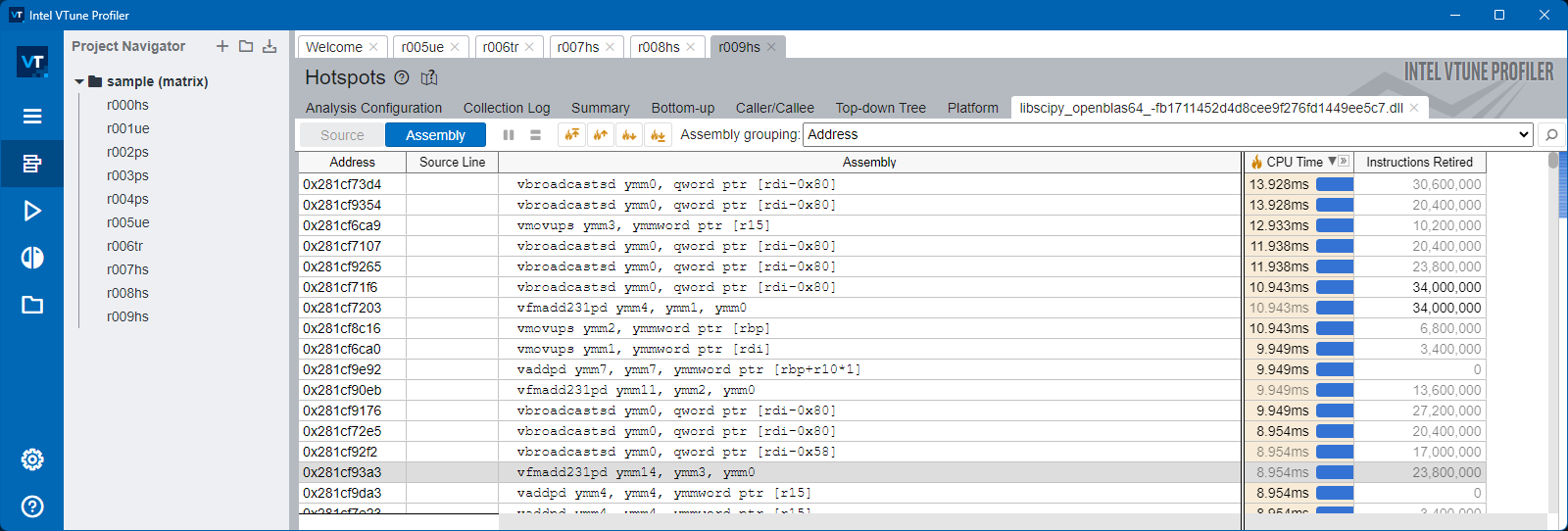
C++ - MSVC

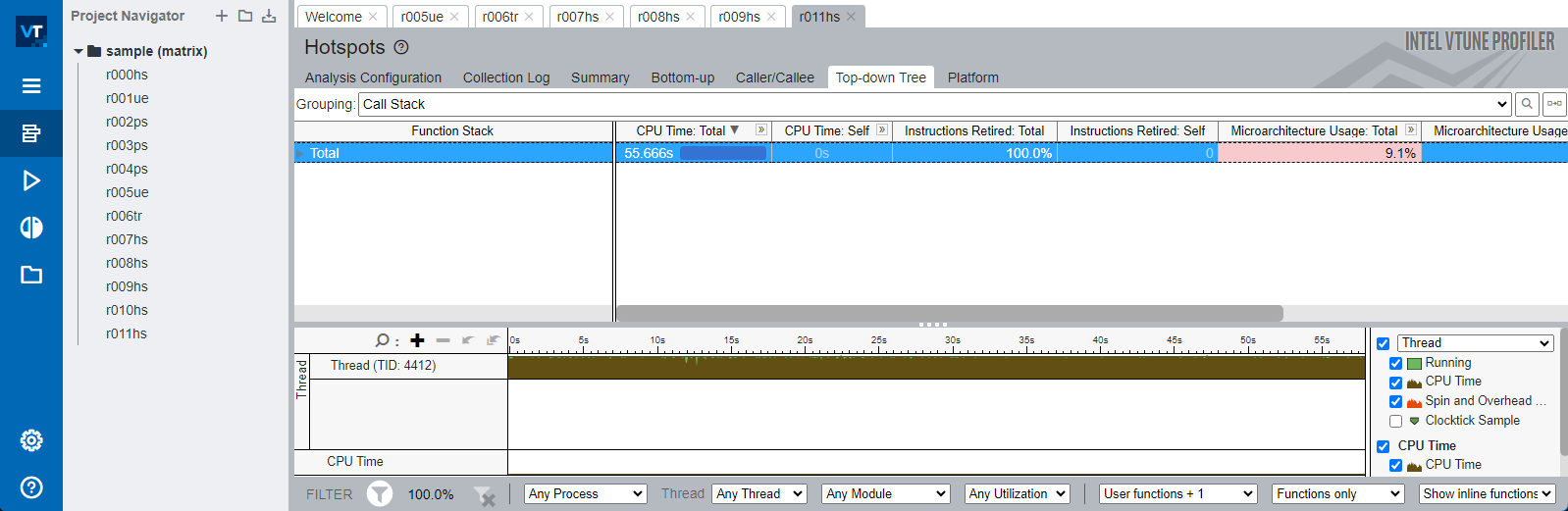
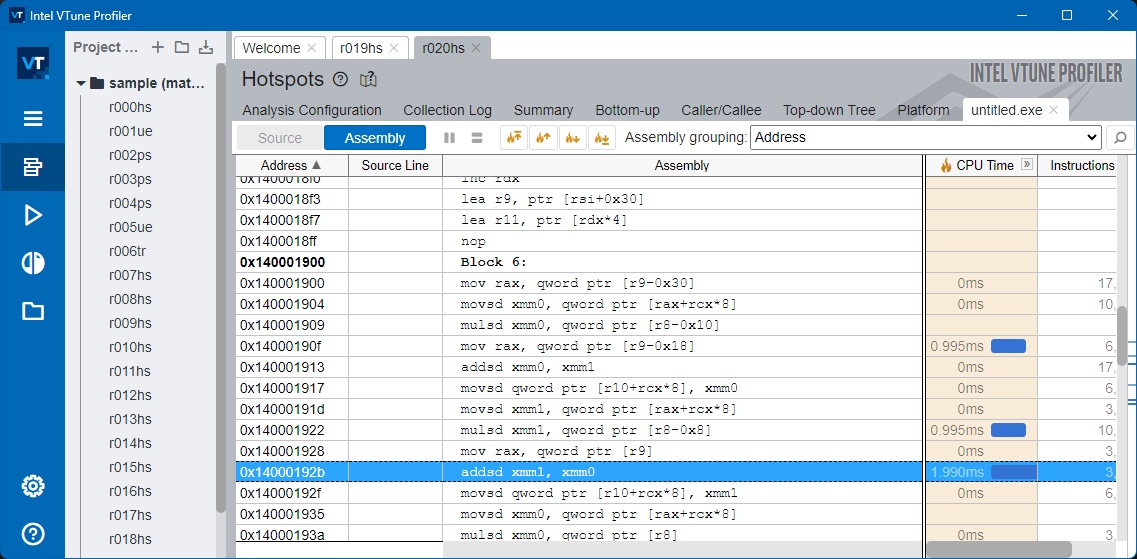
Danger

My Naïve version isn’t using AVX2 but SSE instruction set and isn’t multithreaded

Improving the C++ program

AVX2 and Multithreading with OpenMP

cmake_minimum_required(VERSION 3.28)  
project(SimpleAVX2MP)  
  
set(CMAKE_CXX_STANDARD 17)  
  
# Add optimization flags for Release build type  
if (MSVC)  
    set(CMAKE_CXX_FLAGS_RELEASE "${CMAKE_CXX_FLAGS_RELEASE} /O2 /Ox /Arch:AVX2")  
endif()  
  
# Find OpenMP  
find_package(OpenMP REQUIRED)  
add_executable(SimpleAVX2MP main.cpp)  
  
# Link OpenMP libraries  
if(OpenMP_CXX_FOUND)  
    target_link_libraries(SimpleAVX2MP PUBLIC OpenMP::OpenMP_CXX) 
endif()

#include <iostream>  
#include <vector>  
#include <chrono>  
#include <omp.h>  
  
void matmul(const std::vector<std::vector<double>>& A,  
            const std::vector<std::vector<double>>& B,  
            std::vector<std::vector<double>>& C) {  
    int n = A.size();  
    #pragma omp parallel for  
    for (int i = 0; i < n; ++i) {  
        for (int j = 0; j < n; ++j) {  
            C[i][j] = 0;  
            for (int k = 0; k < n; ++k) {  
                C[i][j] += A[i][k] * B[k][j];  
            }  
        }  
    }  
}  
  
int main() {  
    int n = 3000;  
    std::vector<std::vector<double>> A(n, std::vector<double>(n));  
    std::vector<std::vector<double>> B(n, std::vector<double>(n));  
    std::vector<std::vector<double>> C(n, std::vector<double>(n));  
  
    // Initialize matrices  
    for (int i = 0; i < n; ++i) {  
        for (int j = 0; j < n; ++j) {  
            A[i][j] = rand() / double(RAND_MAX);  
            B[i][j] = rand() / double(RAND_MAX);  
        }  
    }  
  
    auto start = std::chrono::high_resolution_clock::now();  
    matmul(A, B, C);  
    auto end = std::chrono::high_resolution_clock::now();  
  
    std::chrono::duration<double> duration = end - start;  
    std::cout << "Time taken by C++: " << duration.count() << " seconds" << std::endl;  
  
    return 0;  
}

Astuce

Results for C++ / OpenMP / AVX2 : 7.4244 seconds

Using a specialized library like Eigen

cmake_minimum_required(VERSION 3.28)  
project(EigenOpenMPAVX2)  
  
set(CMAKE_CXX_STANDARD 17)  
  
# Add optimization flags for Release build type  
set(CMAKE_CXX_FLAGS_RELEASE "${CMAKE_CXX_FLAGS_RELEASE} /O2 /Ox /Ob3 /arch:AVX2")  
find_package(OpenMP REQUIRED)  
# Add the path to the Eigen directory  
set(EIGEN3_INCLUDE_DIR "C:/Users/remi/CLionProjects/untitled1/eigen")  
# Include the Eigen directory  
include_directories(${EIGEN3_INCLUDE_DIR})  
add_executable(EigenOpenMPAVX2 main.cpp)  
if(OpenMP_CXX_FOUND)  
    target_link_libraries(EigenOpenMPAVX2 PUBLIC OpenMP::OpenMP_CXX)  
    add_definitions(-DEIGEN_USE_THREADS)  
endif()

#include <iostream>  
#include <Eigen/Dense>  
#include <chrono>  
#include <omp.h>  
  
int main() {  
    int n = 3000;  
    Eigen::MatrixXd A = Eigen::MatrixXd::Random(n, n);  
    Eigen::MatrixXd B = Eigen::MatrixXd::Random(n, n);  
    Eigen::MatrixXd C(n, n);  
  
    //Set the number of threads for OpenMP  
    int num_threads = omp_get_max_threads();  
    omp_set_num_threads(num_threads);  
    Eigen::setNbThreads(num_threads);  
  
    std::cout << "Using " << num_threads << " threads for Eigen." << std::endl;  
  
    auto start = std::chrono::high_resolution_clock::now();  
    C.noalias() = A * B; // Use noalias to avoid temporary allocation  
    auto end = std::chrono::high_resolution_clock::now();  
  
    std::chrono::duration<double> duration = end - start;  
    std::cout << "Time taken by Eigen with OpenMP: " << duration.count() << " seconds" << std::endl;  
  
    return 0;  
}

Astuce

Results for C++ / OpenMP / AVX2 / Eigen : 0.2219 seconds

It’s better but not as a fresh install of numpy (10 seconds to install it)

Using OpenBLAS with MinGW

cmake_minimum_required(VERSION 3.15)  
project(OpenBLASExample)  
  
set(CMAKE_CXX_STANDARD 14)  
  
# Define the path to your OpenBLAS installation  
set(OpenBLAS_DIR "C:/Users/remi/CLionProjects/obl/openblas")  
  
# Add the OpenBLAS include and library directories  
include_directories(${OpenBLAS_DIR}/include)  
link_directories(${OpenBLAS_DIR}/lib)  
  
# Add an executable (replace main.cpp with your source file)  
add_executable(OpenBLASExample main.cpp)  
  
# Set compiler optimization flags  
set(COMPILER_OPT_FLAGS "-O3 -march=native -flto -fopenmp")  
  
# Link OpenBLAS library  
target_link_libraries(OpenBLASExample ${OpenBLAS_DIR}/lib/libopenblas.a)

#include <cblas.h>  
#include <iostream>  
#include <chrono>  
  
int main() {  
    const int size = 3000;  
    double *A = new double[size * size];  
    double *B = new double[size * size];  
    double *C = new double[size * size];  
  
    for (int i = 0; i < size * size; ++i) {  
        A[i] = rand() / double(RAND_MAX);  
        B[i] = rand() / double(RAND_MAX);  
    }  
  
    auto start = std::chrono::high_resolution_clock::now();  
    cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans, size, size, size, 1.0, A, size, B, size, 0.0, C, size);  
    auto end = std::chrono::high_resolution_clock::now();  
  
    std::chrono::duration<double> diff = end - start;  
    std::cout << "Time to multiply matrices with OpenBLAS: " << diff.count() << " s\n";  
  
    delete[] A;  
    delete[] B;  
    delete[] C;  
    return 0;  
}

Astuce

Results for C++ / OpenMP / AVX2 / OpenBLAS : 0.1496 s

Using Intel Math Kernel Library

cmake_minimum_required(VERSION 3.28)  
project(MKLProject)  
  
set(CMAKE_CXX_STANDARD 17)  
  
# Add optimization flags for Release build type  
set(CMAKE_CXX_FLAGS_RELEASE "${CMAKE_CXX_FLAGS_RELEASE} /O2 /Ox /Ob3 /arch:AVX2")  
  
include_directories("C:/Program Files (x86)/Intel/oneAPI/compiler/2024.2/include")  
link_directories("C:/Program Files (x86)/Intel/oneAPI/compiler/2024.2/lib")  
# Include the MKL directories (adjust these paths according to your MKL installation)  
include_directories("C:/Program Files (x86)/Intel/oneAPI/mkl/2024.2/include")  
link_directories("C:/Program Files (x86)/Intel/oneAPI/mkl/2024.2/lib")  
  
# Add executable  
add_executable(MKLProject main.cpp)  
  
# Link the MKL libraries  
target_link_libraries(MKLProject PUBLIC mkl_intel_lp64  mkl_intel_thread mkl_core libiomp5md)

#include <iostream>  
#include <chrono>  
#include <mkl.h>  
  
int main() {  
    int n = 3000;  
  
    // Allocate matrices  
    double* A = new double[n * n];  
    double* B = new double[n * n];  
    double* C = new double[n * n];  
  
    // Initialize matrices A and B with random values  
    for (int i = 0; i < n * n; ++i) {  
        A[i] = static_cast<double>(rand()) / RAND_MAX;  
        B[i] = static_cast<double>(rand()) / RAND_MAX;  
        C[i] = 0.0;  
    }  
  
    // Set the number of threads for MKL  
    int num_threads = mkl_get_max_threads();  
    mkl_set_num_threads(num_threads);  
  
    std::cout << "Using " << num_threads << " threads for MKL." << std::endl;  
  
    auto start = std::chrono::high_resolution_clock::now();  
  
    // Perform matrix multiplication using MKL's dgemm function  
    cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans, n, n, n, 1.0, A, n, B, n, 0.0, C, n);  
  
    auto end = std::chrono::high_resolution_clock::now();  
  
    std::chrono::duration<double> duration = end - start;  
    std::cout << "Time taken by MKL for matrix multiplication: " << duration.count() << " seconds" << std::endl;  
  
    // Clean up  
    delete[] A;  
    delete[] B;  
    delete[] C;  
  
    return 0;  
}

Astuce

Results for C++ / Intel MKL : 0.1111 seconds

Working with Cython

Naïve version

from setuptools import setup  
from Cython.Build import cythonize  
  
setup(  
    ext_modules = cythonize("matrix_multiply.pyx")  
)

import cython  
from libc.stdlib cimport malloc, free, rand, RAND_MAX  
from libc.time cimport clock, CLOCKS_PER_SEC  
  
@cython.boundscheck(False)  
@cython.wraparound(False)  
cdef void matmul(double** A, double** B, double** C, int n):  
    cdef int i, j, k  
    for i in range(n):  
        for j in range(n):  
            C[i][j] = 0  
            for k in range(n):  
                C[i][j] += A[i][k] * B[k][j]  
  
def matrix_multiply(int n):  
    cdef int i, j  
    cdef double** A = <double**>malloc(n * sizeof(double*))  
    cdef double** B = <double**>malloc(n * sizeof(double*))  
    cdef double** C = <double**>malloc(n * sizeof(double*))  
    cdef double start, end  
  
    for i in range(n):  
        A[i] = <double*>malloc(n * sizeof(double))  
        B[i] = <double*>malloc(n * sizeof(double))  
        C[i] = <double*>malloc(n * sizeof(double))  
  
    # Initialize matrices  
    for i in range(n):  
        for j in range(n):  
            A[i][j] = rand() / RAND_MAX  
            B[i][j] = rand() / RAND_MAX  
  
    start = clock()  
    matmul(A, B, C, n)  
    end = clock()  
  
    # Free allocated memory  
    for i in range(n):  
        free(A[i])  
        free(B[i])  
        free(C[i])  
    free(A)  
    free(B)  
    free(C)  
  
    return (end - start) / CLOCKS_PER_SEC

Astuce

Results for Cython : 60.487 seconds

With small optimization

from setuptools import setup, Extension  
from Cython.Distutils import build_ext  
  
ext_modules = [  
    Extension(  
        'matrix_multiply2',  
        sources=['matrix_multiply2.pyx'],  
        extra_compile_args=['/openmp', '/O2','/arch:AVX2']  # Enable OpenMP and AVX2  
    )  
]  
  
setup(  
    name='matrix_multiply2',  
    ext_modules=ext_modules,  
    cmdclass={'build_ext': build_ext},  
)

import cython  
from libc.stdlib cimport malloc, free, rand, RAND_MAX  
from libc.time cimport clock, CLOCKS_PER_SEC  
from cython.parallel cimport prange, parallel  
  
@cython.boundscheck(False)  
@cython.wraparound(False)  
cdef void matmul(double** A, double** B, double** C, int n):  
    cdef int i, j, k  
    # Use OpenMP to parallelize the outer loop  
    for i in prange(n, nogil=True,num_threads=16):  
        for j in range(n):  
            C[i][j] = 0  
            for k in range(n):  
                C[i][j] += A[i][k] * B[k][j]  
  
def matrix_multiply(int n):  
    cdef int i, j  
    cdef double** A = <double**>malloc(n * sizeof(double*))  
    cdef double** B = <double**>malloc(n * sizeof(double*))  
    cdef double** C = <double**>malloc(n * sizeof(double*))  
    cdef double start, end  
  
    for i in range(n):  
        A[i] = <double*>malloc(n * sizeof(double))  
        B[i] = <double*>malloc(n * sizeof(double))  
        C[i] = <double*>malloc(n * sizeof(double))  
  
    # Initialize matrices  
    for i in range(n):  
        for j in range(n):  
            A[i][j] = rand() / RAND_MAX  
            B[i][j] = rand() / RAND_MAX  
  
    start = clock()  
    matmul(A, B, C, n)  
    end = clock()  
  
    # Free allocated memory  
    for i in range(n):  
        free(A[i])  
        free(B[i])  
        free(C[i])  
    free(A)  
    free(B)  
    free(C)  
  
    return (end - start) / CLOCKS_PER_SEC

Astuce

Results for Cython / OpenMP / AVX2 : 7.363 seconds

Benchmark results

So to recap :

import matplotlib.pyplot as plt  
import numpy as np  
import matplotlib.colors as mcolors  
  
# Data  
languages = ['Cython - Naive', 'C++ - Naive', 'C++ - AVX2 - OpenMP', 'Cython - AVX2 - OpenMP',  
             'C++ - AVX2 - Eigen - OpenMP', 'C++ - AVX2 - OpenBLAS', 'Python - Numpy (OpenBLAS)', 'C++ - Intel MKL']  
r_times = [60.487, 55.9159, 7.4244, 7.363, 0.2219, 0.1496, 0.1469, 0.1111]  
times = [time + 1 for time in r_times]  
  
times  
log_times = np.log10(times)  
  
plt.figure(figsize=(12, 6))  
  
# Combine language names and times for the labels  
labels = [f'{lang} - {time:.4f}s' for lang, time in zip(languages, r_times)]  
  
# Create a colormap from red to blue  
cmap = plt.get_cmap('prism_r')  
norm = mcolors.Normalize(vmin=min(r_times), vmax=max(r_times))  
colors = [cmap(norm(time)) for time in log_times]  
  
# Create horizontal bar chart  
bars = plt.barh(range(len(languages)), log_times, color=colors)  
# Set the global font size to 14  
plt.rcParams.update({'font.size': 14})  
  
# Add text labels on the bars  
for bar, label in zip(bars, labels):  
    plt.text(0.02, bar.get_y() + bar.get_height() / 2, label, va='center', ha='left', color='black', fontsize=16)  
  
# Remove y-axis labels  
plt.yticks([])  
plt.xlabel('Log of Execution Time in seconds', fontsize=14, labelpad=10)  
plt.ylabel('Implementations', fontsize=14, labelpad=10)  
plt.title('Execution Time of Different Implementations', pad=20, fontsize=20)  
plt.show()

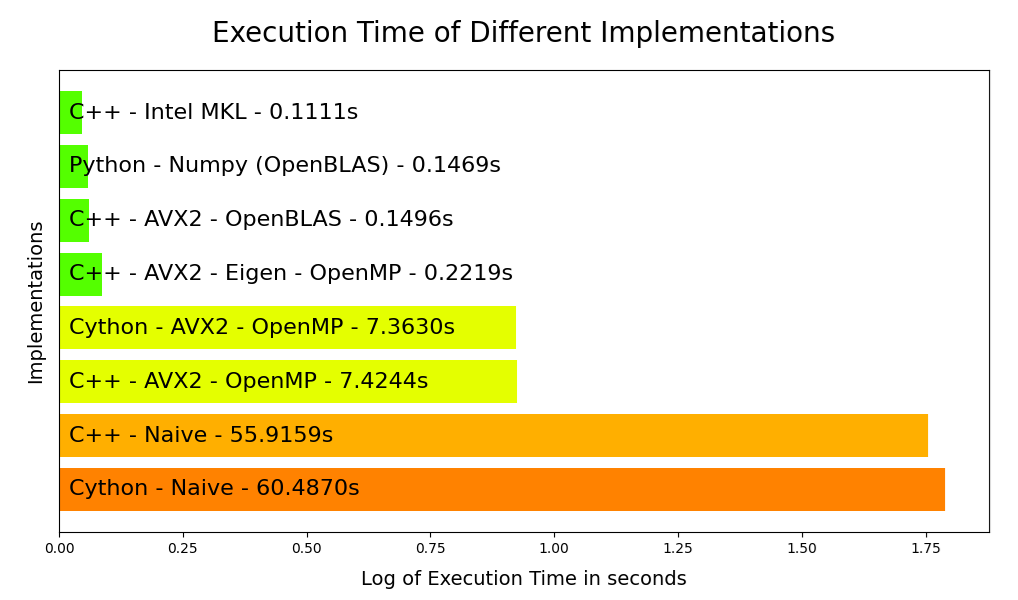
Conclusion

• Clearly, the three lines of code for Numpy are unbeatable. Within a minute, I achieve performance levels that surpass anything I can produce in C++ (except when using Intel MKL, which is a proprietary library).

• C++ allows for complete, meticulous control over what you execute on the processor. However, using a library like OpenBLAS or Intel MKL is akin to using a black box, just like Numpy.

• Talented scientists and engineers have worked on these libraries. Why reinvent the wheel? Why start from scratch as a scientist?

• Python is the perfect tool because it is simple and intuitive for teaching physics. Its performance, when used correctly (with compiled libraries for critical parts), is more than sufficient for any university professor, at least up to a Master’s level.