Marche aléatoire 🍷

Le mouvement brownien, aussi appelé marche aléatoire, revêt une importance particulière dans l’étude de la nature. Il a permis à l’époque de confirmer l’existence des atomes, ainsi que d’évaluer le nombre d’Avogadro. Les recherches associées à ce mouvement sont encore utilisées aujourd’hui dans de nombreux domaines des sciences physiques, mais aussi en finance (notamment pour l’analyse des cours boursiers). On parle alors de processus stochastique. Ces travaux sont associés à des scientifiques prestigieux tels qu’Albert Einstein et Jean Perrin. On se propose dans ce petit papier de modéliser le mouvement brownien suivant une approche élémentaire. On se servira du modèle de l’ivrogne (représentant une particule).[3]

Robert Brown

Robert Brown (1773-1858) était un botaniste écossais célèbre pour sa découverte du mouvement Brownien en 1827. Ce phénomène se réfère à l’agitation aléatoire des particules microscopiques en suspension dans un fluide, qu’il observa en examinant des grains de pollen dans l’eau. Brown croyait initialement que ce mouvement était une caractéristique des particules vivantes, mais il s’est vite rendu compte qu’il se produisait même avec des particules inanimées. Le mouvement Brownien a été fondamental dans le développement de la physique statistique, particulièrement dans les travaux d’Albert Einstein au début du 20e siècle, qui a expliqué ce mouvement par les collisions entre les particules et les molécules de fluide.[1]

Jean Perrin

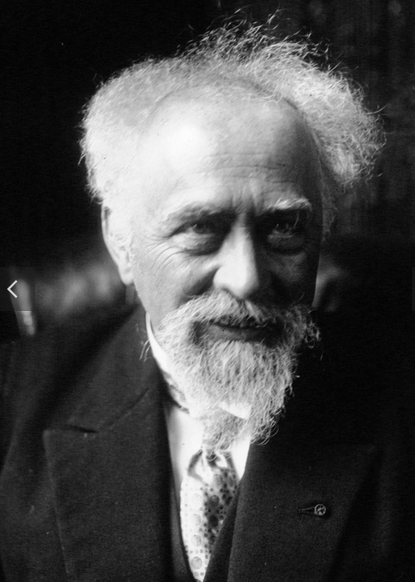
Jean Perrin (1870-1942) était un physicien français Lillois qui a joué un rôle crucial dans la validation expérimentale du mouvement brownien. En 1908, il a confirmé les travaux théoriques d’Albert Einstein sur ce phénomène en étudiant la répartition des particules en suspension dans un liquide. Perrin a démontré que ce mouvement aléatoire des particules était causé par les collisions avec les molécules du liquide, fournissant ainsi une preuve directe de l’existence des atomes et des molécules. Ses travaux ont été essentiels pour établir la théorie atomique, et en 1926, il a reçu le prix Nobel de physique pour ses contributions à la physique moléculaire et atomique.[2]

Présentation du problème

Prudence

L’objectif est de présenter un code simple et compréhensible. Il ne s’agit pas d’optimiser excessivement le code Python 🐍, ni de tirer parti des multiples cœurs des processeurs modernes, et encore moins d’utiliser des bibliothèques comme CUDA, qui permettent le calcul massivement parallèle sur un GPU. Une optimisation sommaire est proposée en annexe.

Dans l’étude du transport de grandeurs physiques par des molécules, le physicien peut, en première approximation, adopter un modèle stochastique appelé marche aléatoire. C’est le cas, par exemple, pour l’interprétation de la viscosité, qui peut être considérée comme le transport d’une quantité de mouvement. Comme mentionné plus haut, le modèle utilisé est celui de l’ivrogne, où celui-ci effectue aléatoirement un pas d’une longueur fixe, notée \(l\), dans un sens ou dans l’autre.

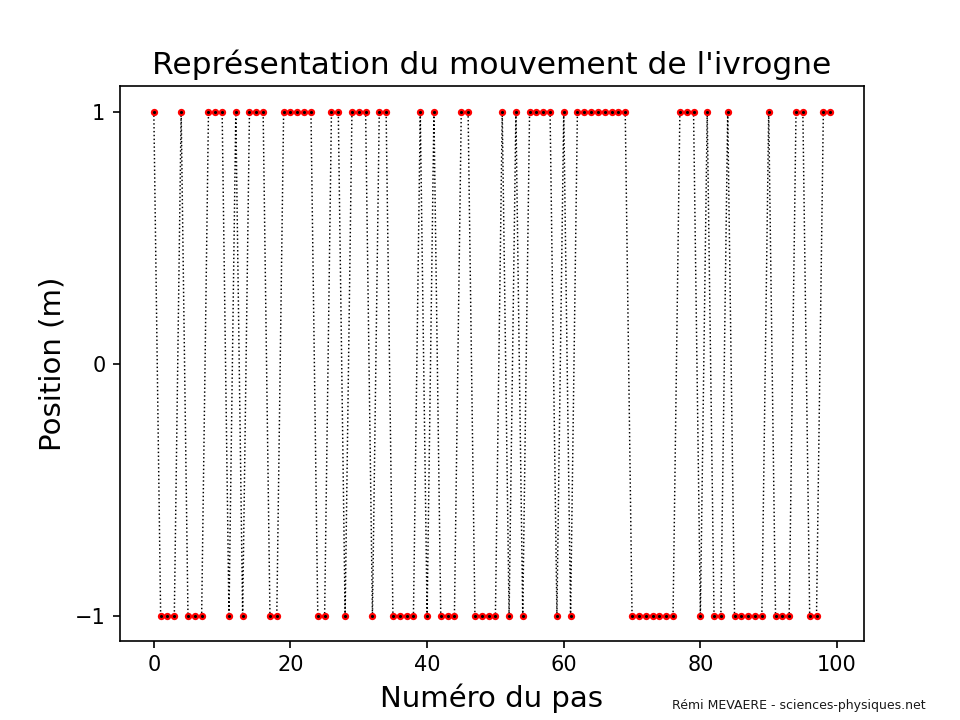
Code 1 - représentation simple du mouvement de l’ivrogne

# Importation des bibliothèques nécessaires  
import random  # Pour générer des valeurs aléatoires  
import matplotlib  # Pour configurer les paramètres globaux de matplotlib  
import matplotlib.pyplot as plt  # Pour créer des graphiques  
  
# Configuration globale de la résolution des graphiques  
matplotlib.rcParams['figure.dpi'] = 150  # Définit la résolution des images/vidéos pour une meilleure qualité visuelle  
  
# Paramètres  
NBR_PAS = 100  # Nombre de pas que fera l'ivrogne dans sa marche aléatoire  
trajectoire = []  # Liste pour stocker les positions à chaque pas  
  
# Génération de la trajectoire avec marche aléatoire (modèle de l'ivrogne)  
position = 0  # Initialisation de la position à 0  
for i in range(NBR_PAS):  
    pas = random.choice([-1, 1])  # L'ivrogne fait un pas de +1m ou -1m (choix aléatoire)  
    trajectoire.append(pas)  # Ajoute le pas à la liste  
  
# Affichage du graphique  
plt.plot(trajectoire, ".:", linewidth=0.7, markersize=5, color="black", markeredgecolor="red")  # Tracé de la courbe  
plt.title("Représentation du mouvement de l'ivrogne",fontsize=15)  # Titre du graphique  
plt.xlabel('Numéro du pas', fontsize=14)  # Étiquette pour l'axe des x (le numéro du pas)  
plt.ylabel('Position (m)', fontsize=14)  # Étiquette pour l'axe des y (la position en mètres)  
plt.yticks(range(min(trajectoire), max(trajectoire) + 1))  # Ajuste les graduations sur l'axe y pour montrer toutes les positions possibles  
plt.figtext(0.70, 0.015, 'Rémi MEVAERE - sciences-physiques.net', fontsize=6, color='black', alpha=0.9, fontweight='normal')  # Ajout d'une mention en bas à droite  
  
# Afficher ou sauvegarder l'image  
plt.show()  # Affiche le graphique à l'écran

Code 2 : Simulation de la trajectoire de 20 ivrognes parcourant 1000 pas

# Mathématiques et calculs  
import random  
  
# Graphiques  
import matplotlib  
import matplotlib.pyplot as plt  
from matplotlib import animation  
  
# Configuration des paramètres de Matplotlib pour les graphiques  
matplotlib.rcParams['animation.html'] = 'html5'  # Configuration pour affichage des animations  
matplotlib.rcParams['figure.dpi'] = 150  # Définition de la résolution des images  
  
# Constantes  
NBR_PAS = 1000  # Nombre de pas par ivrogne  
NBR_IVROGNE = 20  # Nombre d'ivrognes simulés  
trajectoires_ivrognes = []  # Liste pour stocker les trajectoires de chaque ivrogne  
X_MAX = 0  # Variable pour suivre la position maximale  
X_MIN = 0  # Variable pour suivre la position minimale  
  
# Simulation des trajectoires des ivrognes  
for b in range(NBR_IVROGNE):  
    pas = []  # Liste pour stocker les pas individuels  
    trajectoire = []  # Liste pour stocker la trajectoire cumulée  
    # Simulation des pas pour un ivrogne    for i in range(NBR_PAS):  
        pas.append(random.choice([-1, 1]))  # Choix aléatoire d'un pas (-1 ou 1)  
        trajectoire.append(sum(pas))  # Mise à jour de la trajectoire  
    # Enregistrer la trajectoire de cet ivrogne    trajectoires_ivrognes.append(trajectoire)  
    # Mettre à jour les bornes pour l'axe des ordonnées  
    MAX_TRAJ = max(trajectoire)  
    MIN_TRAJ = min(trajectoire)  
    if MAX_TRAJ > X_MAX:  
        X_MAX = MAX_TRAJ  
    if MIN_TRAJ < X_MIN:  
        X_MIN = MIN_TRAJ  
  
# Création d'une liste des numéros de pas pour l'axe des abscisses  
num_pas = [i for i in range(NBR_PAS)]  
  
# Création de la figure et de l'axe pour le graphique  
fig, ax = plt.subplots()  
ax = plt.axis([0, NBR_PAS, X_MIN-2, X_MAX+2])  # Définition des limites de l'axe  
  
# Création des objets "courbe" pour chaque ivrogne  
courbe = []  
for c in range(NBR_IVROGNE):  
    courbe.append(plt.plot([0], [0], '-', linewidth=1, solid_joinstyle='round', label="Ivrogne n°" + str(c)))  # Initialiser les courbes  
  
# Embellissement du graphique  
plt.title("Trajectoire des ivrognes", fontsize=15)  
plt.xlabel('Numéro du pas', fontsize=14)  
plt.ylabel("Position (m)", fontsize=14)  
plt.figtext(0.70, 0.015, 'Rémi MEVAERE - sciences-physiques.net', fontsize=6, color='black', alpha=0.9, fontweight='normal')  # Ajout d'une mention en bas à droite  
  
# Fonction d'animation appelée pour chaque frame  
def animate(i):  
    # Mettre à jour les données pour chaque ivrogne  
    for b in range(NBR_IVROGNE):  
        courbe[b][0].set_data(num_pas[0:i], trajectoires_ivrognes[b][0:i])  # Mettre à jour les points tracés  
  
# Création d'une animation, en créant un graphique image par image  
myAnimation = animation.FuncAnimation(fig, animate, frames=NBR_PAS, interval=20, repeat=False)  
  
# Sauvegarde de l'animation dans un fichier .mp4 (optionnel)  
myAnimation.save("trajectoire_ivrognes.mp4", writer="ffmpeg")  
  
# Affichage du graphique animé  
plt.show()

Problématique

Quelle est la probabilité que l’ivrogne effectue, au total, un déplacement de \(\mathbf{x}\) mètres dans la direction des \(\mathbf{x > 0}\) ?

Résolution

Épreuve de Bernoulli

Nous nous plaçons, comme il est fréquent en physique, dans un cas simplifié. Nous considérons une marche aléatoire unidimensionnelle, décrite le long d’un unique axe \(\mathbf{x}\). Il sera, par la suite, plus aisé de généraliser ce résultat à un mouvement tridimensionnel, plus représentatif de la réalité physique. L’image en en-tête d’ailleurs représente un modèle plus complexe de mouvement stochastique à deux dimensions.

Sur le plan mathématique, nous nous appuierons sur des concepts de probabilité. Chaque déplacement de l’ivrogne correspond à une épreuve, et l’expérience consiste en une succession de \(\mathbf{N}\) épreuves. Chaque épreuve peut conduire à l’un des deux événements équiprobables suivants :

• Événement + : la particule se déplace dans la direction des \(\mathbf{x}\) positifs ;

• Événement - : la particule se déplace dans la direction des \(\mathbf{x}\) négatifs.

Relions \(\mathbf{n}\), le nombre de pas vers la droite (positifs), avec \(\mathbf{N}\) (le nombre total de déplacements) et \(\mathbf{m}\) la position finale sur l’axe des \(x\). La position finale \(m\) est donnée par la différence entre le nombre de pas vers la droite \(n\) et le nombre de pas vers la gauche \((N - n)\) :

\[ m = n - (N - n) = 2n - N \quad \implies \quad n = \frac{m + N}{2}\]

Remarque 🧠

Nous pourrions suivre le même raisonnement en paramétrant les déplacements vers la gauche plutôt que ceux vers la droite ; les résultats finaux seraient identiques. En effet, dans notre modèle, l’ivrogne n’a pas de raison particulière de privilégier un déplacement vers la gauche par rapport à un pas vers la droite (les directions sont équiprobables, \(p_{\pm} = 0{,}5\)).

On peut ensuite se demander quelle est la probabilité d’obtenir \(\mathbf{n}\) déplacements vers la droite parmi \(\mathbf{N}\) épreuves. C’est-à-dire, quelle est la probabilité que l’ivrogne aille \(\mathbf{n}\) fois vers la droite lorsqu’il effectue \(\mathbf{N}\) déplacements au total. La loi binomiale vue en mathématiques au lycée répond à cette question :

\[ \large{p(n, N) =C^{n}_{N}.p^{n}_{+}.p^{N-n}_{-}= \binom{N}{n} \, p_{+}^{\, n} \, p_{-}^{\, N - n}} \]

Notation 🖍️

\(p_{+}^{\, n}\) représente la probabilité d’effectuer un déplacement vers la droite, élevée à la puissance \(n\).

Avec le théorème central limite

Pour calculer la probabilité que l’ivrogne se retrouve en position \(m\) après \(N\) pas, on utilisera le théorème central limite (très utile lorsque \(N\) est grand).

Pourquoi utiliser le théorème central limite ?

Le théorème central limite est fondamental en probabilité et en statistique, il nous permet d’approcher la distribution binomiale par une loi normale (gaussienne), ce qui simplifie les calculs. Il affirme que la somme de variables aléatoires indépendantes et identiquement distribuées tend vers une distribution normale lorsque le nombre de variables augmente.

Pertinence :

• Chaque déplacement élémentaire de l’ivrogne est une variable aléatoire indépendante ;

• Les déplacements sont identiquement distribués (chaque pas a la même probabilité d’être à gauche ou à droite) ;

Intérêt :

• Simplicité de calcul : Au lieu de manipuler des distributions binomiales complexes pour de grandes valeurs de \(N\), on utilise une gaussienne, beaucoup plus facile à gérer analytiquement ;

• Prévision des comportements : Il permet de prédire la probabilité de trouver l’ivrogne à une certaine distance de son point de départ après un grand nombre de pas.

• Universalité : Ce théorème est applicable à de nombreux systèmes physiques où des variables aléatoires indépendantes s’additionnent, comme en physique statistique, en thermodynamique ou en finance.

Variable aléatoire : déplacement élémentaire

Définissons une variable aléatoire nommée déplacement élémentaire notée \(\delta X_i\), ayant deux valeurs possibles \(\delta X_i = \pm 1\) :

• \(\delta X_i = +l\) si l’ivrogne se déplace vers la droite.

• \(\delta X_i = -l\) si l’ivrogne se déplace vers la gauche.

La variable aléatoire \(X_N\), somme des petits déplacements élémentaires représente la position finale \(m\) de l’ivrogne après \(N\) pas :

\[ \large{X_N = \sum_{i=1}^{N} \delta X_i} = m \]

Espérance

\[\begin{split} \begin{align*} \langle \delta X_i \rangle &= p_{+} \times (+1) + p_{-} \times (-1) = p_{+}\times 1 - (1-p_{+})\times 1=2 p_{+} - 1 \\ &= 2 \left( \dfrac{1}{2} \right) - 1 =0 \end{align*} \end{split}\]

Le résultat étant trivial vu que les deux évènements sont équiprobables.

Variance

\[ \langle (\delta X_i)^2 \rangle = p_{+} \times (+1)^2 + p_{-} \times (-1)^2 =p_{+}+(1-p_{+})= 1\]

Ecart-type

\[\sigma_{\delta X}^2= \langle (\delta X_i)^2 \rangle - \langle \delta X_i \rangle^2 = 1\]

Application du Théorème

Le théorème central limite stipule que pour \(N \gg 1\), la variable aléatoire \(X_N\) suit approximativement une loi normale centrée sur \(N \cdot \langle \delta X_i \rangle\) (ici 0) et de variance \(N \cdot \sigma_{\delta X}^2\) (ici \(N\)) :

\[ P(X_N) = \frac{1}{\sqrt{2\pi \cdot N \sigma_{\delta X}^2}} \exp \left[ - \frac{(X_N - N \cdot \langle \delta X_i \rangle )^2}{2 \cdot N \sigma_{\delta X}^2} \right] \]

En remplaçant \(\langle \delta X_i \rangle = 0\) et \(\sigma_{\delta X}^2 = 1\), on obtient :

\[ P(X_N) = \frac{1}{\sqrt{2\pi N}} \exp \left[ - \frac{X_N^2}{2 N} \right] \]

Étant donné que le déplacement net \(m\) est égal à \(X_N\), la probabilité de trouver l’ivrogne en position \(x\) après \(N\) pas est donnée par :

\[ \LARGE\boxed{P(n) = \frac{1}{\sqrt{2\pi N }} \exp \left[ - \dfrac{m^2}{2 N } \right]} \]

Code 3 - Vérification de la distribution normale

Note

Pour la simulation on se facilite la tâche en utilisant un déplacement \(l=\pm 1\)

import numpy as np  
import matplotlib  
import matplotlib.pyplot as plt  
from matplotlib import animation  
  
# Constantes  
NBR_PAS = 100  # Nombre de pas pour chaque ivrogne  
NBR_IVROGNES = 900000  # Nombre total d'ivrognes simulés  
  
# Configuration des paramètres de Matplotlib pour les graphiques  
matplotlib.rcParams['animation.html'] = 'html5'  # Configuration pour affichage des animations  
matplotlib.rcParams['figure.dpi'] = 150  # Définition de la résolution des images  
  
# Simulation des positions finales des ivrognes  
deplacements = np.random.choice([-1, 1], size=(NBR_IVROGNES, NBR_PAS))  
positions_finales = np.sum(deplacements, axis=1)  
  
# Détermination des positions minimale et maximale pour ajuster les limites du graphique  
MIN, MAX = positions_finales.min(), positions_finales.max()  
  
# Préparation de la figure pour l'animation  
fig, ax = plt.subplots()  
ax.set_xlim(MIN - 5, MAX + 5)  
plt.xlabel('Position finale', fontsize=12)  
plt.ylabel("Probabilité", fontsize=12)  
plt.title('Distribution des positions finales des ivrognes')  
  
plt.figtext(0.70, 0.015, 'sciences-physiques.net', fontsize=6, color='black', alpha=0.9,  
            fontweight='normal')  
  
# Initialisation de l'histogramme  
nombre_bandes = MAX - MIN + 1  
  
# Calcul de la courbe gaussienne théorique  
x_gauss = np.linspace(MIN, MAX, 1000)  
P_gauss = (1 / np.sqrt(2 * np.pi * NBR_PAS)) * np.exp(-x_gauss ** 2 / (2 * NBR_PAS))  
  
  
# Fonction d'animation pour mettre à jour l'histogramme  
def animer_histogramme(i):  
    plt.cla()  # Efface le contenu précédent de la figure  
    donnees_histogramme = positions_finales[0:i]  # Sélectionne les positions jusqu'à l'ivrogne i  
  
    # Tracer l'histogramme normalisé (probabilités)    comptes, bandes, patches = plt.hist(donnees_histogramme, bins=nombre_bandes, range=(MIN - 0.5, MAX + 0.5),  
                                        density=True, facecolor='blue', alpha=0.5, edgecolor='black')  
  
    # Calcul de la largeur des bandes  
    largeur_bande = bandes[1] - bandes[0]  
  
    # Tracer la courbe théorique gaussienne ajustée à la largeur des bandes  
    plt.plot(x_gauss, P_gauss * largeur_bande * 2, color='red', lw=2, label='Gaussienne théorique')  
  
    # Mise à jour des paramètres de la figure  
    plt.title(f"Distribution des positions finales : {i} ivrogne(s)", fontsize=15)  
    plt.xlabel('Position finale', fontsize=14)  
    plt.ylabel("Probabilité", fontsize=14)  
    plt.xlim(MIN - 5, MAX + 5)  
    plt.ylim(0, max(comptes.max(), (P_gauss * largeur_bande).max()) * 1.1)  # Ajustement dynamique des ordonnées  
  
  
# Création de la liste des frames pour l'animation  
liste_frames = (  
        list(range(1, 11)) +  
        [i * 10 for i in range(2, 11)] +  
        [i * 100 for i in range(2, 11)] +  
        [i * 1000 for i in range(2, 11)] +  
        [i * 10000 for i in range(2, NBR_IVROGNES // 10000 + 1)]  
)  
  
# Ajustement des marges pour laisser de l'espace autour des axes  
plt.subplots_adjust(left=0.15, right=0.95, top=0.9, bottom=0.1)  
  
# Création de l'animation en utilisant la fonction animer_histogramme  
mon_animation = animation.FuncAnimation(fig, animer_histogramme, frames=liste_frames, interval=200, repeat=False)  
  
# Optionnel : sauvegarde de l'animation dans un fichier vidéo  
mon_animation.save("distribution_ivrognes.mp4", writer="ffmpeg")  
  
# Affichage de l'animation  
plt.show()

Probabilité de parcourir une distance \(x\)

Revenons à l’ivrogne. Nous cherchons à connaître la distance \(\mathbf{x}\) parcourue après une durée déterminée \(\mathbf{\Delta t}\). On se rappelle que \(\mathbf{m}\) est la position finale en nombre de pas (la différence entre le nombre de pas vers la droite et vers la gauche). Les relations entre ces grandeurs sont (\(l\) est la longueur d’un pas) :

\[\mathbf{x} = m \times l\]

De plus, la durée totale est donnée par (\(N\) est le nombre total de pas, \(\tau\) est la durée d’un pas) :

\[ \Delta t = N \times \tau \]

En utilisant ces relations, on peut exprimer la probabilité de trouver l’ivrogne à une distance \(x\) après un temps \(\Delta t\). À partir de la distribution obtenue précédemment pour \(P(m)\), en remplaçant \(m\) par \(\dfrac{x}{l}\), on obtient :

\[P(m) = \frac{1}{\sqrt{2\pi N}} \exp\left( - \frac{m^2}{2N} \right) \quad \implies \quad \large\boxed{{P(x) \frac{1}{\sqrt{2\pi N}} \exp\left( - \frac{x^2}{2 N l^2} \right)}}\]

Sachant que \(N = \dfrac{\Delta t}{\tau}\), on peut aussi écrire :

\[P(x) = \frac{1}{\sqrt{2\pi \dfrac{\Delta t}{\tau}}} \exp\left( - \frac{x^2}{2 \dfrac{\Delta t}{\tau} l^2} \right) = \frac{1}{\sqrt{2\pi \dfrac{\Delta t}{\tau}}} \exp\left( - \frac{\tau x^2}{2 \Delta t l^2} \right) = \dfrac{1}{\sqrt{2\pi \dfrac{\Delta t}{\tau}}} \exp\left[ - \dfrac{\tau x^2}{2 \Delta t l^2} \right]\]

Distance quadratique moyenne parcourue

Nous souhaitons calculer la valeur moyenne de \(x^2\), notée \(\langle x^2 \rangle\), qui est donnée par :

\[ \large\langle x^2 \rangle = \int_{-\infty}^{+\infty} x^2 P(x) \, dx \]

Mais étant donné que \(P(x)\) est une distribution gaussienne centrée en \(0\), nous savons que (\(\sigma^2\) est la variance de la distribution), l’identification est aisée :

\[ \langle x^2 \rangle = \sigma^2 = N l^2 = \left( \dfrac{\Delta t}{\tau} \right) l^2 \]

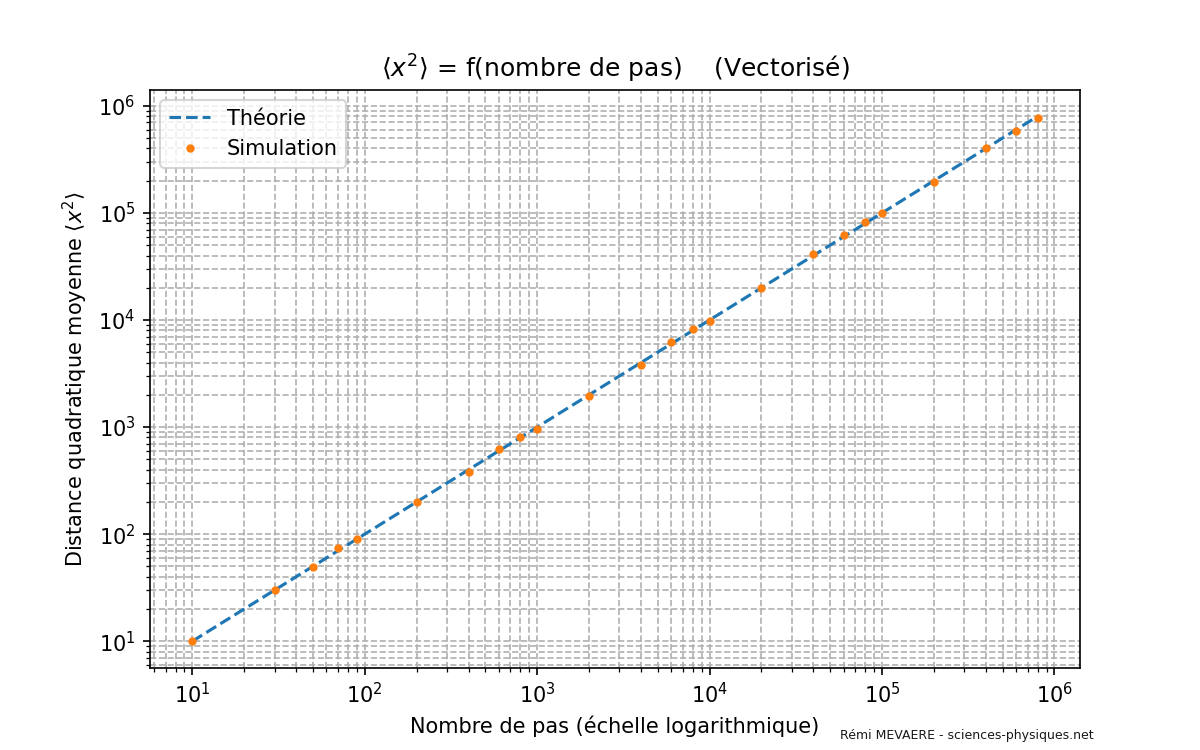
Ainsi, la distance quadratique moyenne parcourue est (\(l>0\), \(\Delta t>0\), \(\tau >0\)) :

\[ \boxed{x_q = \sqrt{\langle x^2 \rangle} = l \sqrt{\dfrac{\Delta t}{\tau}}= l \cdot N} \]

Interprétation physique

La distribution s’élargit proportionnellement à la racine carrée de la durée \(\Delta t\). Autrement dit, la région visitée par la particule (l’ivrogne) croît comme la racine carrée de la durée de l’expérience. Ce comportement est caractéristique d’un processus de diffusion, où la dispersion des particules augmente avec le temps de manière proportionnelle à \(\sqrt{\Delta t}\).

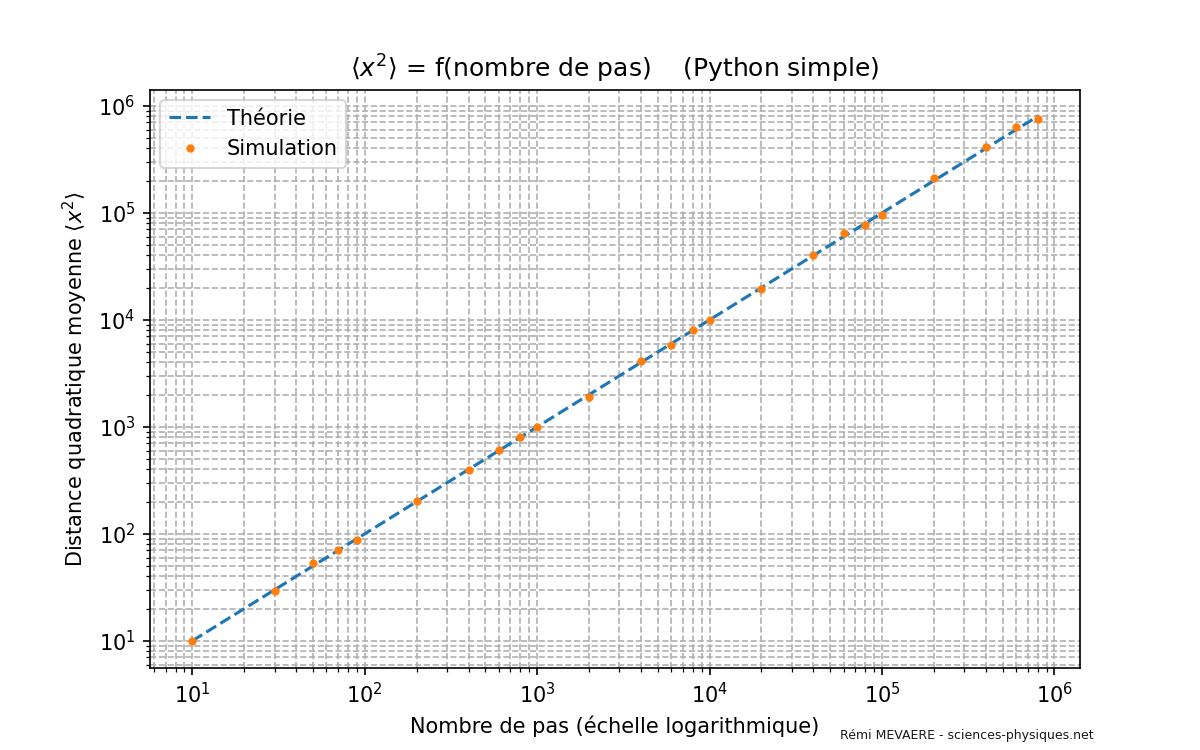
Code 4 - Accord avec la théorie

Optimization 🔩

Sur mon ordinateur, ce code absolument pas optimisé prend une durée très longue (plus de 16 minutes). Les versions Vectorisée et CUDA disponibles en Annexes sont beaucoup plus rapides (40 secondes et 3 secondes).

import random  
import numpy as np  
import matplotlib  
import matplotlib.pyplot as plt  
  
# Configuration des paramètres de Matplotlib pour les graphiques  
matplotlib.rcParams['figure.dpi'] = 150  # Résolution des images  
  
# Constantes  
NBR_IVROGNES = 2000  # Nombre d'ivrognes simulés  
liste_NBR_PAS = (  
    list(range(10, 110, 20)) +  
    list(range(200, 1100, 200)) +  
    list(range(2000, 11000, 2000)) +  
    list(range(20000, 110000, 20000)) +  
    list(range(200000, 1000000, 200000))  
)  
distances_quadratiques_moyennes = []  # Liste pour stocker les distances quadratiques moyennes  
distances_theoriques = []  # Liste pour stocker les distances théoriques  
  
# Simulation pour chaque nombre de pas  
for NBR_PAS in liste_NBR_PAS:  
    positions_finales = []  # Liste pour stocker les positions finales des ivrognes  
    # Simulation des ivrognes    for _ in range(NBR_IVROGNES):  
        position = 0  # Position initiale  
        # Simulation des pas pour un ivrogne        for _ in range(NBR_PAS):  
            pas = random.choice([-1, 1])  # Choix aléatoire d'un pas (-1 ou 1)  
            position += pas  # Mise à jour de la position  
        positions_finales.append(position)  
    # Calcul de la distance quadratique moyenne pour ce nombre de pas  
    distances_quadratiques = [pos**2 for pos in positions_finales]  
    distance_quadratique_moyenne = sum(distances_quadratiques) / NBR_IVROGNES  
    distances_quadratiques_moyennes.append(distance_quadratique_moyenne)  
    # Calcul de la distance théorique  
    distance_theorique = NBR_PAS  # Pour une marche aléatoire simple en 1D  
    distances_theoriques.append(distance_theorique)  
  
# Conversion en tableaux numpy pour faciliter le tracé  
liste_NBR_PAS_np = np.array(liste_NBR_PAS)  
distances_quadratiques_moyennes_np = np.array(distances_quadratiques_moyennes)  
distances_theoriques_np = np.array(distances_theoriques)  
  
# Création du graphique  
plt.figure(figsize=(8, 5))  
plt.plot(liste_NBR_PAS_np, distances_theoriques_np, '--', label='Théorie')  
plt.plot(liste_NBR_PAS_np, distances_quadratiques_moyennes_np, 'o', label='Simulation', markeredgewidth=2, markersize=2)  
plt.xscale('log')  
plt.yscale('log')  
plt.xlabel('Nombre de pas (échelle logarithmique)', fontsize=14)  
plt.ylabel('Distance quadratique moyenne $\\langle x^2 \\rangle$', fontsize=14)  
plt.title('$\\langle x^2 \\rangle$ = f(nombre de pas)    (Python Simple)', fontsize=15)  
plt.legend()  
plt.grid(True, which="both", ls="--")  
plt.figtext(0.70, 0.015, 'www.sciences-physiques.net', fontsize=6, color='black', alpha=0.9, fontweight='normal')  
plt.show()

Conclusion

La distance quadratique moyenne parcourue par l’ivrogne est proportionnelle à \(\sqrt{\Delta t}\), ce qui signifie que la zone explorée s’étend de plus en plus lentement avec le temps. Ce résultat est fondamental pour comprendre les phénomènes de diffusion et de transport dans divers domaines scientifiques. Il illustre comment une succession de déplacements aléatoires conduit à une dispersion des positions qui suit une loi gaussienne. Le fait que la largeur de la distribution augmente comme \(\sqrt{\Delta t}\) est une caractéristique clé des processus diffusifs, tels que la diffusion des particules en physique ou la propagation des erreurs en statistiques.

Annexes

Mathématiques

Intégrale \(I\)

La première intégrale à calculer est :

\[ I = \int^{\infty}_{-\infty} exp(- \alpha x^2) dx \]

En prenant au carré l’intégrale

\[ I^2 = \int^{\infty}_{-\infty} exp(- \alpha x^2) dx \times \int^{\infty}_{-\infty} exp(- \alpha y^2) dy = \int^{\infty}_{-\infty} \int^{\infty}_{-\infty} exp[- \alpha (x^2 + y^2)] dx dy \]

On s’empresse de passer en coordonnée polaire :

\[ I^2 = \int^{\infty}_0 \int^{2\pi}_0 exp(-\alpha r^2) \, r dr d \theta \]

\[ I^2 = \int^{\infty}_0 exp(-\alpha r^2) \, r dr \times \int^{2\pi}_0 d \theta \]

Que l’on sait calculer facilement après un changement de variable (\(u=r^2\)) :

\[ I^2 = \frac{1}{2} \int^{\infty}_0 exp(-\alpha u) du \times \int^{2\pi}_0 d \theta = \pi \int^{\infty}_0 exp(-\alpha u) du= - \frac{\pi}{\alpha} \left[exp(-\alpha u) \right]^\infty_0 \]

La racine carrée donne le résultat de l’intégrale :

\[ \large\boxed{I = \int^{\infty}_{-\infty} exp(- \alpha x^2) dx = \sqrt{\frac{\pi}{\alpha}}} \]

Intégrale \(J\)

\[ J = \int^{\infty}_{-\infty} x^2 exp(- \alpha x^2)\, dx \]

Or l’intégrale \(J\) est l’opposée de la dérivée de \(I\) par rapport à \(\alpha\), c’est à dire :

\[ J = - \frac{d I}{d \alpha} = \int^{\infty}_{-\infty} x^2 exp(- \alpha x^2)\, dx \]

\[ J = \int^{\infty}_{-\infty} x^2 exp(- \alpha x^2) dx= - \frac{d }{d \alpha} \left(\sqrt{\frac{\pi}{\alpha}} \right) \]

\[ \large\boxed{J =\frac{1}{2} \sqrt{\frac{\pi}{\alpha^3}}} \]

Compléments sur la Gaussienne

Une distribution gaussienne classique a la forme :

\[ \large P(x) = \dfrac{1}{\sqrt{2\pi \sigma^2}} \exp\left( - \dfrac{(x - \mu)^2}{2 \sigma^2} \right) \]

l’espérance \(\langle x \rangle = \mu\) et la variance \(\sigma^2\) sont données par :

\[ \large \langle x \rangle = \int_{-\infty}^{+\infty} x P(x) \, dx = \mu \quad \text{et} \quad \large \langle x^2 \rangle - \langle x \rangle^2 = \sigma^2 \]

Dans le cas de cet article, la gaussienne est centrée en 0 (\(\mu = 0\)), donc :

\[ \langle x^2 \rangle = \sigma^2 \]

Formule de Stirling

L”approximation de Stirling est une formule qui donne une estimation de la factorielle d’un grand nombre \(N\). Elle est extrêmement utile en mathématiques et en physique, notamment en probabilités et en statistiques. L’approximation est donnée par :

\[ N! \approx N^N e^{-N} \sqrt{2\pi N} \]

La factorielle d’un entier naturel \(N\) est défini comme le produit de tous les entiers de \(1\) à \(N\) :

\[ N! = 1 \times 2 \times 3 \times \dots \times N \]

Pour des valeurs de \(N\) grandes, calculer \(N!\) directement devient rapidement impraticable en raison de la taille énorme des nombres impliqués.

Logarithme du factorielle Pour faciliter les manipulations mathématiques, il est souvent utile de travailler avec le logarithme de la factorielle plutôt que la factorielle elle-même. En prenant le logarithme naturel de \(N!\), nous obtenons :

\[ \ln N! = \ln(1 \times 2 \times 3 \times \dots \times N) = \sum_{k=1}^N \ln k \]

Cette somme peut être difficile à calculer directement, mais pour de grandes valeurs de \(N\), nous pouvons l’approcher en utilisant une intégrale. L’idée est d’approximer la somme discrète par une intégrale continue. En effet, pour une fonction suffisamment régulière, la somme des valeurs de la fonction en des points discrets peut être approchée par l’intégrale de cette fonction. Ainsi, nous avons :

\[ \sum_{k=1}^N \ln k \approx \int_{1}^{N} \ln x \, dx \]

\[ \int_{1}^{N} \ln x \, dx = [x \ln x - x]_1^{N} = (N \ln N - N) - (1 \ln 1 - 1) = N \ln N - N + 1 \]

Comme \(\ln 1 = 0\), le terme \(1 \ln 1\) disparaît, et nous obtenons :

\[ \ln N! \approx N \ln N - N + 1 \]

Pour de grandes valeurs de \(N\), le terme constant \(+1\) est négligeable, donc :

\[ \ln N! \approx N \ln N - N \]

Ajout du terme de correction avec la formule d’Euler-Maclaurin

La formule d’Euler-Maclaurin est donnée par :

\[ \sum_{k=a}^{b} f(k) = \int_{a}^{b} f(x) \, dx + \frac{f(a) + f(b)}{2} + \sum_{n=1}^{m} \frac{B_{2n}}{(2n)!} \left( f^{(2n-1)}(b) - f^{(2n-1)}(a) \right) + R_m \]

• \(B_{2n}\) sont les nombres de Bernoulli

• \(R_m\) est le reste après \(m\) termes.

Pour notre approximation, nous négligeons les termes d’ordre supérieur (de plus les dérivées impaires de \(\ln x\) diminuent rapidement et les nombres de Bernoulli alternent en signe et diminuent en magnitude, nous négligeons donc ces termes pour \(N\) grand) et le reste \(R_m\) il ne reste que le terme moyen de correction à ajouter :

\[ \frac{f(1) + f(N)}{2} = \frac{\ln 1 + \ln N}{2} = \frac{0 + \ln N}{2} = \frac{\ln N}{2} \]

\[ \ln N! \approx N \ln N - N + \frac{1}{2} \ln N \]

Revenons à \(N!\) en prenant l’exponentielle des deux côtés :

\[ N! \approx e^{N \ln N - N + \frac{1}{2} \ln N} = e^{N \ln N - N} \cdot e^{\frac{1}{2} \ln N} \]

\[ N! \approx e^{N \ln N - N} \cdot \sqrt{N} \]

\[ e^{N \ln N - N} = N^N e^{-N} \quad \implies \quad N! \approx N^N e^{-N} \sqrt{N}\]

Méthode de Laplace pour approximation plus précise

L’approximation de Stirling complète inclut un facteur \(\sqrt{2\pi N}\) pour améliorer la précision, surtout pour des valeurs de \(N\) moins grandes. Pour justifier l’apparition de ce facteur, nous pouvons utiliser la méthode de Laplace.

La factorielle est liée à la fonction Gamma par :

\[N! = \Gamma(N+1) = \int_{0}^{\infty} x^N e^{-x} \, dx = \int_{0}^{\infty} e^{N \ln x - x} \, dx\]

Nous allons appliquer la méthode de Laplace à cette intégrale :

\[I = \int_{0}^{\infty} e^{N f(x)} \, dx \implies f(x) = \ln x - \frac{x}{N}\]

Trouver le maximum de \(f(x)\)

\[f'(x) = \frac{1}{x} - \frac{1}{N}\]

\[f'(x)=0 \implies \frac{1}{x} - \frac{1}{N} = 0 \implies x = N\]

\[f''(x) = -\frac{1}{x^2} \implies f''(N) = -\frac{1}{N^2}\]

Le développement de Taylor de \(f(x)\) autour de \(x = N\) est :

\[f(x) \approx f(N) + \frac{f''(N)}{2} (x - N)^2 = \ln N - 1 - \frac{1}{2N^2} (x - N)^2\]

\[N f(x) \approx N (\ln N - 1) - \frac{(x - N)^2}{2N}\]

L’intégrale devient :

\[I \approx e^{N f(N)} \int_{-\infty}^{\infty} e^{-\frac{(x - N)^2}{2N}} \, dx\]

Remarque : Nous avons étendu les bornes d’intégration à \((-\infty, \infty)\) car la contribution significative provient d’une région étroite autour de \(x = N\) pour \(N\) grand.

L’intégrale est une intégrale gaussienne connue :

\[\int_{-\infty}^{\infty} e^{-\frac{(x - N)^2}{2N}} \, dx = \sqrt{2\pi N}\]

En combinant les résultats, nous obtenons :

\[I \approx e^{N f(N)} \sqrt{2\pi N} = e^{N \ln N - N} \sqrt{2\pi N}\]

Comme \(I = N!\), nous obtenons l’approximation de Stirling complète :

\[N! \approx N^N e^{-N} \sqrt{2\pi N}\]

Physique

Démonstration avec la formule de Stirling

\[ \large{p(n, N) =C^{n}_{N}.p^{n}_{+}.p^{N-n}_{-}= \binom{N}{n} \, p_{+}^{\, n} \, p_{-}^{\, N - n}} \]

Pour calculer la probabilité que l’ivrogne se retrouve en position \(m\) après \(N\) pas, nous allons utiliser l”approximation de Stirling pour simplifier le calcul du coefficient binomial lorsque \(N\) est grand.

Approximation de Stirling

Pour des grands nombres \(N\), l’approximation de Stirling pour la factorielle est donnée par :

\[ N! \approx N^N e^{-N} \sqrt{2\pi N} \quad \implies \quad \ln N! \approx N \ln N - N + \frac{1}{2} \ln(2\pi N) \]

Calcul du logarithme de la probabilité

\[ p(n, N) = \frac{N!}{n! (N - n)!} \left( \frac{1}{2} \right)^N \quad \implies \quad \ln p(n, N) = \ln N! - \ln n! - \ln (N - n)! - N \ln 2 \]

\[\begin{split} \begin{align*} \ln N! &\approx N \ln N - N + \frac{1}{2} \ln(2\pi N) \\ \ln n! &\approx n \ln n - n + \frac{1}{2} \ln(2\pi n) \\ \ln (N - n)! &\approx (N - n) \ln (N - n) - (N - n) + \frac{1}{2} \ln [2\pi (N - n)] \end{align*} \end{split}\]

Substituons ces expressions dans \(\ln p(n, N)\) :

\[\begin{split} \begin{align*} \ln p(n, N) &\approx [N \ln N - N + \frac{1}{2} \ln(2\pi N)] \\ &\quad - [n \ln n - n + \frac{1}{2} \ln(2\pi n)] \\ &\quad - [(N - n) \ln (N - n) - (N - n) + \frac{1}{2} \ln(2\pi (N - n))] \\ &\quad - N \ln 2 \end{align*} \end{split}\]

\[\begin{split} \begin{align*} \ln p(n, N) &\approx N \ln N - N - n \ln n + n - (N - n) \ln (N - n) + (N - n) \\ &\quad + \frac{1}{2} \ln(2\pi N) - \frac{1}{2} \ln(2\pi n) - \frac{1}{2} \ln[2\pi (N - n)] - N \ln 2 \end{align*} \end{split}\]

\[ \large\boxed{\ln p(n, N) \approx N \ln N - n \ln n - (N - n) \ln (N - n) - N \ln 2} \]

Ecriture avec les grandeurs du problème

Nous pouvons écrire \(n\) et \(N - n\) en fonction de \(N\) et \(m\) :

\[ m = n - (N - n) = 2n - N \quad \implies \quad n = \frac{m + N}{2} \quad \text{et} \quad N - n = \frac{N - m}{2}\]

\[ \begin{align*} \ln p(m, N) &\approx N \ln N - \left( \frac{N + m}{2} \right) \ln \left( \frac{N + m}{2} \right) - \left( \frac{N - m}{2} \right) \ln \left( \frac{N - m}{2} \right) - N \ln 2 \end{align*} \]

\[ \begin{align*} \ln p(m, N) &\approx N \ln N - \frac{N + m}{2} [\ln (N + m) - \ln 2] - \frac{N - m}{2} [\ln (N - m) - \ln 2] - N \ln 2 \end{align*} \]

\[ \ln p(m, N) \approx N \ln N - \frac{N + m}{2} \ln (N + m) + \frac{N + m}{2} \ln 2 = - \frac{N - m}{2} \ln (N - m) + \frac{N - m}{2} \ln 2 - N \ln 2 \]

\[\ln p(m, N) \approx N \ln N - \frac{N + m}{2} \ln (N + m) - \frac{N - m}{2} \ln (N - m) \quad + \left[ \left( \frac{N + m}{2} + \frac{N - m}{2} - N \right) \ln 2 \right]\]

\[ \large\boxed{\ln p(m, N) \approx N \ln N - \frac{N + m}{2} \ln (N + m) - \frac{N - m}{2} \ln (N - m)} \]

Développement limité pour \(m \ll N\)

Lorsque \(N\) est grand et \(m \ll N\), nous pouvons développer les logarithmes en utilisant l’approximation de Taylor :

Voici le développement de Taylor de \(\ln(1 + x)\) au voisinage de 0 en Markdown :

Le développement de Taylor de \(\ln(1 + x)\) au voisinage de 0 est donné par :

\[ \ln(1 + x) = \sum_{n=1}^\infty (-1)^{n+1} \dfrac{x^n}{n} = x - \dfrac{x^2}{2} + \dfrac{x^3}{3} - \dfrac{x^4}{4} + \dfrac{x^5}{5} - \dots \]

\[\ln\left(1 \pm \frac{m}{N}\right) \approx \pm \frac{m}{N} - \frac{1}{2} \left( \frac{m}{N} \right)^2\]

\[ \ln(N \pm m) = \ln\left(N \left(1 \pm \frac{m}{N}\right)\right) = \ln N + \ln\left(1 \pm \frac{m}{N}\right) \]

\[ \ln(N \pm m) \approx \ln N + \left( \pm \frac{m}{N} - \frac{1}{2} \left( \frac{m}{N} \right)^2 \right) = \ln N \pm \frac{m}{N} - \frac{m^2}{2N^2} \]

Calculons chaque terme séparément de

\[ \ln p(m, N) \approx N \ln N - \frac{N + m}{2} \ln (N + m) - \frac{N - m}{2} \ln (N - m) \]

Premier terme :

\[ N \ln N \]

Deuxième terme :

\[\begin{split} \begin{align*} \frac{N + m}{2} \ln (N + m) &\approx \left( \frac{N}{2} + \frac{m}{2} \right) \left( \ln N + \frac{m}{N} - \frac{m^2}{2N^2} \right) \\ &= \frac{N}{2} \ln N + \frac{N}{2} \left( \frac{m}{N} \right) + \frac{N}{2} \left( - \frac{m^2}{2N^2} \right) \\ &\quad + \frac{m}{2} \ln N + \frac{m}{2} \left( \frac{m}{N} \right) - \frac{m}{2} \left( \frac{m^2}{2N^2} \right) \\ &= \frac{N}{2} \ln N + \frac{m}{2} + \left( - \frac{m^2}{4N} \right) + \frac{m}{2} \ln N + \frac{m^2}{2N} - \frac{m^3}{4N^2} \end{align*} \end{split}\]

Troisième terme :

\[\begin{split} \begin{align*} \frac{N - m}{2} \ln (N - m) &\approx \left( \frac{N}{2} - \frac{m}{2} \right) \left( \ln N - \frac{m}{N} - \frac{m^2}{2N^2} \right) \\ &= \frac{N}{2} \ln N - \frac{N}{2} \left( \frac{m}{N} \right) - \frac{N}{2} \left( \frac{m^2}{2N^2} \right) \\ &\quad - \frac{m}{2} \ln N + \frac{m}{2} \left( \frac{m}{N} \right) + \frac{m}{2} \left( \frac{m^2}{2N^2} \right) \\ &= \frac{N}{2} \ln N - \frac{m}{2} - \left( \frac{m^2}{4N} \right) - \frac{m}{2} \ln N + \frac{m^2}{2N} + \frac{m^3}{4N^2} \end{align*} \end{split}\]

Regroupement des termes :

\[\begin{split} \begin{align*} \ln p(m, N) &\approx N \ln N \\ &\quad - \left[ \frac{N}{2} \ln N + \frac{m}{2} + \frac{m}{2} \ln N - \frac{m^2}{4N} + \frac{m^2}{2N} - \frac{m^3}{4N^2} \right] \\ &\quad - \left[ \frac{N}{2} \ln N - \frac{m}{2} - \frac{m}{2} \ln N - \frac{m^2}{4N} + \frac{m^2}{2N} + \frac{m^3}{4N^2} \right] \end{align*} \end{split}\]

Simplification des termes :

Les termes en \(N \ln N\) :

\[ N \ln N - \left( \frac{N}{2} \ln N + \frac{N}{2} \ln N \right) = N \ln N - N \ln N = 0 \]

Les termes en \(m\) :

\[ - \left( \frac{m}{2} + \left( - \frac{m}{2} \right) \right) = - \left( \frac{m}{2} - \frac{m}{2} \right) = 0 \]

Les termes en \(m \ln N\) :

\[ - \left( \frac{m}{2} \ln N + \left( - \frac{m}{2} \ln N \right) \right) = - \left( \frac{m}{2} \ln N - \frac{m}{2} \ln N \right) = 0 \]

Les termes en \(m^2\) :

\[ - \left( + \frac{m^2}{4N} + \frac{m^2}{4N} \right) = -\frac{m^2}{2N} \]

Les termes en \(m^3\) sont négligeables pour \(m \ll N\) et peuvent être ignorés.

Ainsi

\[ \ln p(m, N) \approx -\frac{m^2}{2N} \]

Probabilité

\[ \large\boxed{p(m, N) \approx e^{- \frac{m^2}{2N}}} \]

Ce résultat montre que la probabilité suit une distribution gaussienne centrée en \(m = 0\) avec une variance proportionnelle à \(N\), ce qui est conforme au théorème central limite pour une marche aléatoire.

Facteur de normalisation

Pour normaliser la fonction, nous utilisons l’intégrale gaussienne :

\[ I = \int_{-\infty}^{\infty} e^{- \alpha x^2} dx = \sqrt{\frac{\pi}{\alpha}}. \]

Dans notre cas, \(\alpha = \dfrac{1}{2N}\), donc :

\[ \int_{-\infty}^{\infty} e^{- \frac{m^2}{N}} dm = \sqrt{2\pi N}.\]

Le facteur de normalisation est donc \(\dfrac{1}{\sqrt{\pi N}}\). Ainsi, la densité de probabilité normalisée est :

\[ P(m) = \frac{1}{\sqrt{2\pi N}} e^{- \frac{m^2}{2N}}. \]

La probabilité de trouver l’ivrogne en position \(m\) après \(N\) pas est donnée par :

\[ \large\boxed{P(m) = \frac{1}{\sqrt{2\pi N}} \exp \left( - \dfrac{m^2}{2N} \right)} \]

Intérêt de l’approximation de Stirling ici

L’utilisation de l’approximation de Stirling est particulièrement utile lorsque le nombre de pas \(N\) est grand. Elle permet de simplifier les calculs en remplaçant les factorielles par des expressions plus faciles à manipuler.

Dans le cas de l’ivrogne :

• Simplicité de calcul : Elle évite le calcul direct de factorielles de grands nombres, qui peut être complexe et impraticable.

• Approche asymptotique : Elle fournit une approximation valable pour \(N \gg 1\), ce qui est souvent le cas dans les problèmes physiques et statistiques.

• Lien avec la loi normale : Elle permet de montrer que la distribution binomiale tend vers une loi normale lorsque \(N\) est grand, ce qui est une manifestation du théorème central limite.

Code

Version vectorisée

# Importation des bibliothèques nécessaires  
import numpy as np  
import matplotlib  
import matplotlib.pyplot as plt  
  
# Configuration des paramètres de Matplotlib pour les graphiques  
matplotlib.rcParams['figure.dpi'] = 150  # Résolution des images  
  
# Constantes  
NBR_IVROGNES = 2000  
liste_NBR_PAS = (  
        list(range(10, 110, 20)) +  
        list(range(200, 1100, 200)) +  
        list(range(2000, 11000, 2000)) +  
        list(range(20000, 110000, 20000)) +  
        list(range(200000, 1000000, 200000))  
)  
distances_quadratiques_moyennes = []  # Liste pour stocker les distances quadratiques moyennes  
distances_theoriques = []  # Liste pour stocker les distances théoriques  
  
# Simulation pour chaque nombre de pas  
for NBR_PAS in liste_NBR_PAS:  
    # Génération de tous les pas aléatoires en une seule fois  
    pas = np.random.choice([-1, 1], size=(NBR_IVROGNES, NBR_PAS))  
    # Calcul des positions finales en sommant les pas  
    positions_finales = pas.sum(axis=1)  
    # Calcul de la distance quadratique moyenne pour ce nombre de pas  
    distances_quadratiques = positions_finales ** 2  
    distance_quadratique_moyenne = distances_quadratiques.mean()  
    distances_quadratiques_moyennes.append(distance_quadratique_moyenne)  
    # Calcul de la distance théorique  
    distance_theorique = NBR_PAS  # Pour une marche aléatoire simple en 1D  
    distances_theoriques.append(distance_theorique)  
  
# Conversion en tableaux numpy pour faciliter le tracé  
liste_NBR_PAS_np = np.array(liste_NBR_PAS)  
distances_quadratiques_moyennes_np = np.array(distances_quadratiques_moyennes)  
distances_theoriques_np = np.array(distances_theoriques)  
  
# Création du graphique  
plt.figure(figsize=(8, 5))  
plt.plot(liste_NBR_PAS_np, distances_theoriques_np, '--', label='Théorie')  
plt.plot(liste_NBR_PAS_np, distances_quadratiques_moyennes_np, 'o', label='Simulation', markeredgewidth=2, markersize=2)  
plt.xscale('log')  
plt.yscale('log')  
plt.xlabel('Nombre de pas (échelle logarithmique)')  
plt.ylabel('Distance quadratique moyenne $\\langle x^2 \\rangle$')  
plt.title('$\\langle x^2 \\rangle$ = f(nombre de pas)    (Vectorisé)')  
plt.legend()  
plt.grid(True, which="both", ls="--")  
plt.figtext(0.70, 0.015, 'www.sciences-physiques.net', fontsize=6, color='black', alpha=0.9, fontweight='normal')  
plt.show()

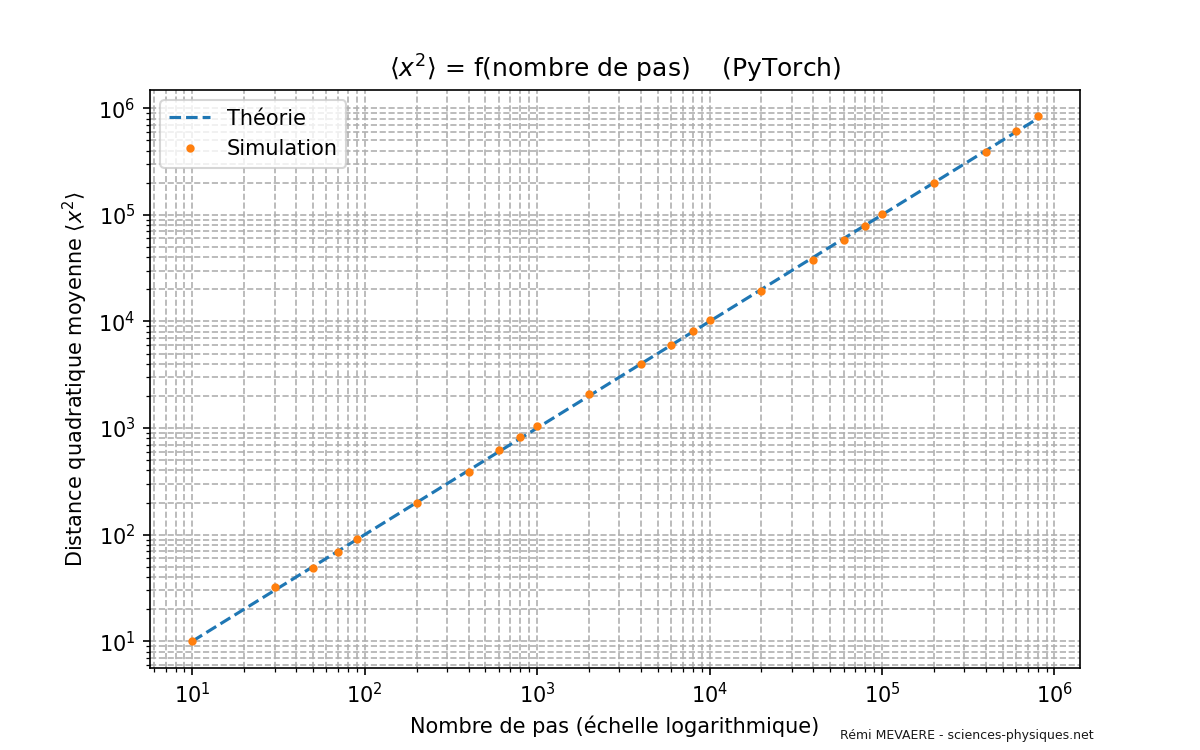
Version utilisant pytorch et CUDA (de NVidia)

# Importation des bibliothèques nécessaires  
import torch  
import matplotlib  
import matplotlib.pyplot as plt  
  
# Configuration des paramètres de Matplotlib pour les graphiques  
matplotlib.rcParams['figure.dpi'] = 150  # Résolution des images  
  
# Détection du dispositif (CPU ou GPU)  
dispositif = torch.device('cuda' if torch.cuda.is_available() else 'cpu')  
print(f"Utilisation du dispositif : {dispositif}")  
  
# Constantes  
NBR_IVROGNES = 2000  
liste_NBR_PAS = (  
        list(range(10, 110, 20)) +  
        list(range(200, 1100, 200)) +  
        list(range(2000, 11000, 2000)) +  
        list(range(20000, 110000, 20000)) +  
        list(range(200000, 1000000, 200000))  
)  
distances_quadratiques_moyennes = []  # Liste pour stocker les distances quadratiques moyennes  
distances_theoriques = []  # Liste pour stocker les distances théoriques  
  
# Simulation pour chaque nombre de pas  
for NBR_PAS in liste_NBR_PAS:  
    # Génération de tous les pas aléatoires en une seule fois sur le dispositif choisi  
    pas = torch.randint(0, 2, (NBR_IVROGNES, NBR_PAS), device=dispositif, dtype=torch.int8) * 2 - 1  
    # Calcul des positions finales en sommant les pas  
    positions_finales = pas.sum(dim=1)  
    # Calcul de la distance quadratique moyenne pour ce nombre de pas  
    distances_quadratiques = positions_finales.float() ** 2  
    distance_quadratique_moyenne = distances_quadratiques.mean().item()  
    distances_quadratiques_moyennes.append(distance_quadratique_moyenne)  
    # Calcul de la distance théorique  
    distance_theorique = NBR_PAS  # Pour une marche aléatoire simple en 1D  
    distances_theoriques.append(distance_theorique)  
  
# Conversion en tensors pour faciliter le tracé  
liste_NBR_PAS_tensor = torch.tensor(liste_NBR_PAS)  
distances_quadratiques_moyennes_tensor = torch.tensor(distances_quadratiques_moyennes)  
distances_theoriques_tensor = torch.tensor(distances_theoriques)  
  
# Création du graphique  
plt.figure(figsize=(8, 5))  
plt.plot(liste_NBR_PAS_tensor.numpy(), distances_theoriques_tensor.numpy(), '--', label='Théorie')  
plt.plot(liste_NBR_PAS_tensor.numpy(), distances_quadratiques_moyennes_tensor.numpy(), 'o', label='Simulation',  
         markeredgewidth=2, markersize=2)  
plt.xscale('log')  
plt.yscale('log')  
plt.xlabel('Nombre de pas (échelle logarithmique)')  
plt.ylabel('Distance quadratique moyenne $\\langle x^2 \\rangle$')  
plt.title('$\\langle x^2 \\rangle$ = f(nombre de pas)    (PyTorch)')  
plt.legend()  
plt.grid(True, which="both", ls="--")  
plt.figtext(0.70, 0.015, 'www.sciences-physiques.net', fontsize=6, color='black', alpha=0.9, fontweight='normal')  
plt.show()

Sources et autres liens

---

[1]

Biographie de Robert Brown

[2]

Biographie de Jean Perrin

[3]

Vidéo de Science-questions